如图，在平面直角坐标系中，二次函数y=ax2+6x+c的图象经过点A（4，0）、B（﹣1，0），与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=
，EF⊥OD，垂足为F．
（1）求这个二次函数的解析式；
（2）求线段EF、OF的长（用含t的代数式表示）；
（3）当△ECA为直角三角形时，求t的值．
黄冈市三运会期间，武穴黄商有一种姚明牌运动装每件的销售价y（元）与时间x（周）之间的函数关系式对应的点都在如图所示的图象上，该图象从左至右，依次是线段AB、线段BC、线段CD，而这种运动装每件的进价Z（元）与时间x（周）之间的函数关系式为Z=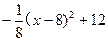
(1≤x≤16且x为整数) 
（1）写出每件的销售价y（元）与时间x（周）之间的函数关系式；
（2）设每件运动装销售利润为w，写出w（元）与时间x（周）之间的函数关系式；
（3）求该运动装第几周出销时，每件运动装的销售利润最大？最大利润为多少？
如图1，等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上，CF>BC，取线段AE的中点M 。
（1）求证：MD=MF,MD⊥MF(6分)
（2）若Rt△CEF绕点C顺时针旋转任意角度（如图2），其他条件不变。（1）中的结论是否仍然成立，若成立，请证明，若不成立，请说明理由。
 |
 |
||
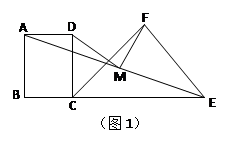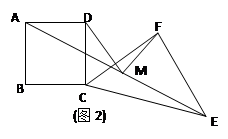边长为整数的直角三角形，若其两直角边边长是方程x2-(k+2)x+4k=0的两根，求k的值，并确定直角三角形三边之长。
下图是行列间隔都为1个单位的点阵：
①你能计算点阵中多边形的面积吗？请将答案直接填入图中横线上。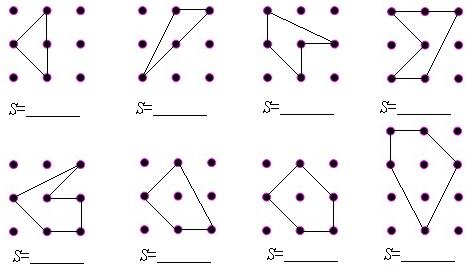
②若用a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积，你能用含a和b的代数式表示S= ____________________
③请你利用②中的公式来求a=4，b=20时，多边形的面积S。
（本题8分）已知有理数
满足①
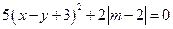；②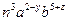
是一个三次单项式且系数为-1：
(1)求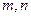
的值； (2)求代数式
的值.