如图，△ABC中，ABAC，AD，CD分别是△ABC两个外角-优题课

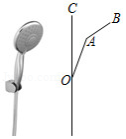
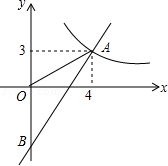
图1是挂墙式淋浴花洒的实物图，图2是抽象出来的几何图形．为使身高 $175 cm$ 的人能方便地淋浴，应当使旋转头固定在墙上的某个位置 $O$ ，花洒的最高点 $B$ 与人的头顶的铅垂距离为 $15 cm$ ，已知龙头手柄 $OA$ 长为 $10 cm$ ，花洒直径 $AB$ 是 $8 cm$ ，龙头手柄与墙面的较小夹角 $∠ COA = 26 °$ ， $∠ OAB = 146 °$ ，则安装时，旋转头的固定点 $O$ 与地面的距离应为多少？（计算结果精确到 $1 cm$ ，参考数据： $\sin 26 ° \approx 0.44$ ， $\cos 26 ° \approx 0.90$ ， $\tan 26 ° \approx 0.49)$

如图，一次函数 $y = kx + b$ 的图象分别与反比例函数 $y = \frac{a}{x}$ 的图象在第一象限交于点 $A (4, 3)$ ，与 $y$ 轴的负半轴交于点 $B$ ，且 $OA = OB$ ．

（1）求函数 $y = kx + b$ 和 $y = \frac{a}{x}$ 的表达式；

（2）已知点 $C (0, 5)$ ，试在该一次函数图象上确定一点 $M$ ，使得 $MB = MC$ ，求此时点 $M$ 的坐标．

"学而时习之，不亦说乎？"古人把经常复习当作是一种乐趣．某校为了解九年级（一 $)$ 班学生每周的复习情况，班长对该班学生每周的复习时间进行了调查，复习时间四舍五入后只有4种：1小时，2小时，3小时，4小时，已知该班共有50人，根据调查结果，制作了两幅不完整的统计图表，该班女生一周的复习时间数据（单位：小时）如下：

1，1，1，2，2，2，2，2，2，2，3，3，3，3，4，4，4，4，4，4

九年级（一 $)$ 班女生一周复习时间频数分布表

复习时间	频数（学生人数）
1小时	3
2小时	$a$
3小时	4
4小时	6

（1）统计表中 $a =$ 　　，该班女生一周复习时间的中位数为　　小时；

（2）扇形统计图中，该班男生一周复习时间为4小时所对应圆心角的度数为　　 $°$ ；

（3）该校九年级共有600名学生，通过计算估计一周复习时间为4小时的学生有多少名？

（4）在该班复习时间为4小时的女生中，选择其中四名分别记为 $A$ ， $B$ ， $C$ ， $D$ ，为了培养更多学生对复习的兴趣，随机从该四名女生中选取两名进行班会演讲，请用树状图或者列表法求恰好选中 $B$ 和 $D$ 的概率．

（1）解不等式组 $\{\begin{matrix} 3 (x - 1) < 5 x + 2 ① \\ \frac{x - 2}{2} ⩽ 7 - \frac{3}{2} x② \end{matrix}$ ，并求出该不等式组的最小整数解．

（2）先化简，再求值： $(\frac{a^{2} - 1}{a^{2} - 2 a + 1} - \frac{1}{1 - a}) \div \frac{2}{a^{2} - a}$ ，其中 $a$ 满足 $a^{2} + 2 a - 15 = 0$ ．

如图，矩形 $ABCD$ 中，点 $P$ 为对角线 $AC$ 所在直线上的一个动点，连接 $PD$ ，过点 $P$ 作 $PE ⊥ PD$ ，交直线 $AB$ 于点 $E$ ，过点 $P$ 作 $MN ⊥ AB$ ，交直线 $CD$ 于点 $M$ ，交直线 $AB$ 于点 $N$ ． $AB = 4 \sqrt{3}$ ， $AD = 4$ ．

（1）如图1，①当点 $P$ 在线段 $AC$ 上时， $∠ PDM$ 和 $∠ EPN$ 的数量关系为： $∠ PDM$ $∠ EPN$ ；

② $\frac{DP}{PE}$ 的值是　　；

（2）如图2，当点 $P$ 在 $CA$ 延长线上时，（1）中的结论②是否成立？若成立，请证明；若不成立，说明理由；

（3）如图3，以线段 $PD$ ， $PE$ 为邻边作矩形 $PEFD$ ．设 $PM$ 的长为 $x$ ，矩形 $PEFD$ 的面积为 $y$ ．请直接写出 $y$ 与 $x$ 之间的函数关系式及 $y$ 的最小值．