为了让学生了解文明礼仪知识，增强文明意识，养成文明习惯。某中学在“文明礼仪，从我做起”知识普及活动中，举行了一次“文明礼仪知识”竞赛，共有3000名学生参加了这次竞赛。为了了解本次竞赛的成绩情况，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行了统计。
频率分布表
| 组别 |
分组 |
频数 |
频率 |
| 1 |
50.5～60.5 |
6 |
0.08 |
| 2 |
60.5～70.5 |
9 |
0.12 |
| 3 |
70.5～80.5 |
15 |
m |
| 4 |
80.5～90.5 |
24 |
0.32 |
| 5 |
90.5～100.5 |
n |
0.28 |
| 合计 |
|
|
|
频数分布直方图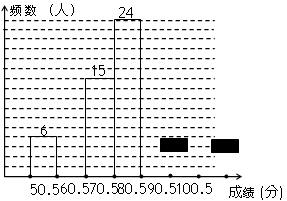
请你根据上面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
（1）求频率分布表中的m、n；
（2）补全频数分布直方图；
（3）你能根据所学知识确定“众数”落在哪一组吗？“中位数”在哪一组吗？
已知抛物线的顶点坐标是（8，9），且过点
，求该抛物线的解析式。
解方程（2x－3）2=x2
在梯形ABCD中，AD∥BC，BA⊥AC，∠ABC = 450，AD = 2，BC = 6，以BC所在直线为x轴，建立如图所示的平面直角坐标系，点A在y轴上.
（1）求过A、D、C三点的抛物线的解析式；
（2）求△ADC的外接圆的圆心M的坐标，并求⊙M的半径；
（3）E为抛物线对称轴上一点，F为y轴上一点，求当ED＋EC＋FD＋FC最小时，EF的长；
（4）设Q为射线CB上任意一点，点P为对称轴左侧抛物线上任意一点，问是否存在这样的点P、Q，使得以P、Q、C为顶点的三角形与△ADC相似？若存在，直接写出点P、Q的坐标，若不存在，则说明理由.
对于三个数a、b、c，M{a，b，c}表示这三个数的平均数，min{a，b，c}表示a、b、c这三个数中最小的数，如：M{－1，2，3}
，min{－1，2，3}＝－1；M{－1，2，a}＝
，min {－1，2，a}＝
解决下列问题：
（1）填空：min{sin30°，cos45°，tan30°}＝________；若min{2，2x＋2，4－2x}＝2，则x的取值范围是________；
（2）①若M{2，x＋1，2x}＝min{2，x＋1，2x}，那么x＝________；
②根据①，你发现结论“若M{a，b，c}＝min{a，b，c}，那么________”（填a，b，c大小关系）；
③运用②，填空：若M{2x＋y＋2，x＋2y，2x－y}＝min{2x＋y＋2，x＋2y，2x－y}，则x＋y＝________；
（3）在同一直角坐标系中作出函数y＝x＋1，y＝（x－1）2，y＝2－x的图象（不需列表，描点），通过图象，得出min{x＋1，（x－1）2，2－x}最大值为________．
受国内外复杂多变的经济环境影响，去年1至7月，原材料价格一路攀升，长沙市某服装厂每件衣服原材料的成本y1（元）与月份x（1≤x≤7，且x为整数）之间的函数关系如下表：
| 月份x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 成本（元/件） |
56 |
58 |
60 |
62 |
64 |
66 |
68 |
8至12月，随着经济环境的好转，原材料价格的涨势趋缓，每件原材料成本y2（元）与月份x的函数关系式为y2=x+62（8≤x≤12，且x为整数）．
（1）请观察表格中的数据，用学过的函数相关知识求y1与x的函数关系式．
（2）若去年该衣服每件的出厂价为100元，生产每件衣服的其他成本为8元，该衣服在1至7月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤7，且x为整数）； 8至12月的销售量p2（万件）与月份x满足关系式p2=﹣0.1x+3（8≤x≤12，且x为整数），该厂去年哪个月利润最大？并求出最大利润．