如图,抛物线 (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似?若存在,求点P的坐标;若不存在,请说明理由.
一快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日净收入.(日净收入=每天的销售额-套餐成本-每天固定支出)
(1)求y与x的函数关系式;
(2)若每份套餐售价不超过10元,要使该店日净收入不少于800元,那么每份售价最少不低于多少元?
(3)该店既要吸引顾客,使每天销售量较大,又要有较高的日净收入.按此要求,每份套餐的售价应定为多少元?此时日净收入为多少?
如图,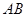 是半圆
是半圆 的直径,过点
的直径,过点 作弦
作弦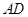 的垂线交半圆
的垂线交半圆 于点
于点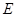 ,交
,交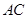 于点
于点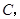 使
使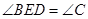 .
.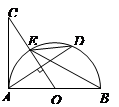
(1)判断直线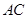 与圆
与圆 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若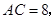
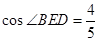 ,求
,求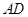 的长.
的长.
现有一个种植总面积为540m2的矩形塑料大棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
| 占地面积(m2/垄) |
产量(千克/垄) |
利润(元/千克) |
|
| 西红柿 |
30 |
160 |
1.1 |
| 草莓 |
15 |
50 |
1.6 |
(1)若设草莓共种植了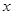 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
有三张背面完全相同的卡片,它们的正面分别写上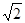 、
、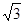 、
、 ,把它们的背面朝上洗匀后;小丽先从中抽取一张,然后小明从余下的卡片中再抽取一张.
,把它们的背面朝上洗匀后;小丽先从中抽取一张,然后小明从余下的卡片中再抽取一张.
(1)直接写出小丽取出的卡片恰好是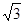 的概率;
的概率;
(2)小刚为他们设计了一个游戏规则:若两人抽取卡片上的数字之积是有理数,则小丽获胜;否则小明获胜.你认为这个游戏规则公平吗?若不公平,则对谁有利?请用画树状图或列表法进行分析说明.
如图,在四边形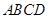 中,点
中,点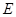 是线段
是线段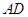 上的任意一点(
上的任意一点(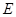 与
与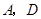 不重合),
不重合),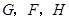 分别是
分别是 的中点.
的中点.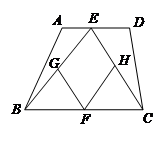
(1)试判断四边形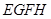 的形状并说明理由;
的形状并说明理由;
(2)在(1)的条件下,若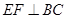 ,且
,且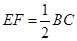 ,证明平行四边形
,证明平行四边形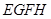 是正方形.
是正方形.