根据2012年国民经济和社会发展统计公报中相关数据,绘制关于全国公共财政收入的统计图的一部分: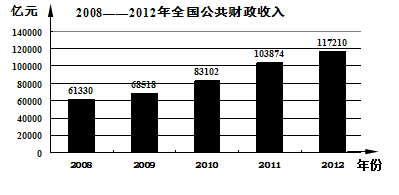
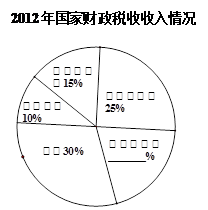
请根据以上信息,解答下列问题
(1)请补全扇形统计图;
(2)通过计算与比较,与上一年相比,财政收入增加最少的是_________年;
(3)由统计图可知,2012年全国财政收入117210亿元;其中,国家财政税收收入比国家财政非税收收入多83992亿元,请你结合统计图,直接计算出,2012年国家财政出口退税____________亿元;
(4)2008——2012这四年间,每年比上一年增长的财政收入的平均数为多少亿元?若按此平均数增长,请你预测2013年全国公共财政收入多少亿元? (精确到亿位)
附加题:本题满分10分.已知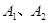 是平面内两个定点,且
是平面内两个定点,且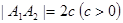 ,若动点
,若动点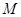 与
与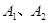 连线的斜率之积等于常数
连线的斜率之积等于常数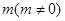 ,求点
,求点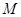 的轨迹方程,并讨论轨迹形状与
的轨迹方程,并讨论轨迹形状与 值的关系.
值的关系.
(本小题满分14分) 已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在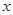 轴上,离心率等于
轴上,离心率等于 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线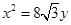 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)点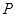
 ,
, ,
, 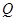
 ,
, 在椭圆上,
在椭圆上,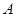 、
、 是椭圆上位于直线
是椭圆上位于直线 两侧的动点.
两侧的动点.
①若直线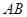 的斜率为
的斜率为 ,求四边形
,求四边形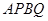 面积的最大值;
面积的最大值;
②当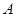 、
、 运动时,满足于
运动时,满足于 ,试问直线
,试问直线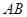 的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
的斜率是否为定值?若是,请求出定值,若不是,请说明理由.
(本小题满分13分) 已知抛物线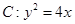 与直线
与直线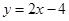 交于
交于 ,
, 两点.
两点.
(Ⅰ)求弦 的长度;
的长度;
(Ⅱ)若点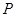 在抛物线
在抛物线 上,且
上,且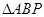 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标.
(本小题满分12分)已知点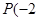 ,
,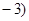 ,圆
,圆 :
: ,过
,过 点作圆
点作圆 的两条切线,切点分别为
的两条切线,切点分别为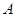 、
、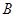 .
.
(Ⅰ)求过 、
、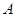 、
、 三点的圆的方程;
三点的圆的方程;
(Ⅱ)求直线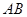 的方程.
的方程.
(本小题满分12分) 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取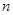 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 ,
,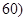 的学生人数为6.
的学生人数为6.
(Ⅰ)求直方图中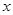 的值;
的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩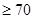 ”的概率.
”的概率.