如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往救援,同时把消息告之在甲船的南偏西30°,相距10海里C处的乙船.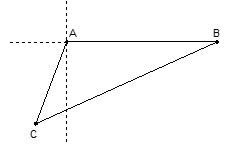
(1)求处于C处的乙船和遇险渔船间的距离;
(2)设乙船沿直线CB方向前往B处救援,求∠ACB的正弦值.
已知函数  .
.
(Ⅰ)求函数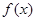 的单调增区间;
的单调增区间;
(Ⅱ)在 中,内角
中,内角 所对边分别为
所对边分别为 ,
,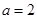 ,若对任意的
,若对任意的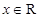 不等式
不等式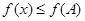 恒成立,求
恒成立,求 面积的最大值.
面积的最大值.
已知函数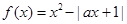 ,
,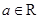 .
.
(1)若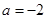 ,且存在互不相同的实数
,且存在互不相同的实数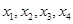 满足
满足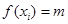
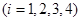 ,求实数
,求实数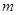 的取值范围;
的取值范围;
(2)若函数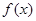 在
在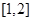 上单调递增,求实数
上单调递增,求实数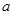 的取值范围.
的取值范围.
已知抛物线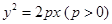 焦点为F,抛物线上横坐标为
焦点为F,抛物线上横坐标为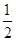 的点到抛物线顶点的距离与其到准线的距离相等.
的点到抛物线顶点的距离与其到准线的距离相等.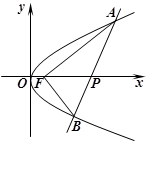
(1)求抛物线的方程;
(2)设过点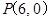 的直线
的直线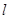 与抛物线交于
与抛物线交于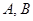 两点,若以
两点,若以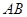 为直径的圆过点
为直径的圆过点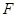 ,求直线
,求直线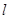 的方程.
的方程.
如图,在三棱锥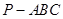 中,
中,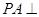 平面
平面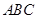 ,
,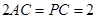 ,
,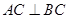 ,
, 、
、 、
、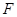 分别为
分别为 、
、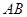 、
、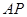 的中点,
的中点, 、
、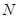 分别为线段
分别为线段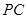 、
、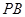 上的动点,且有
上的动点,且有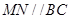 .
.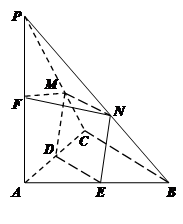
(1)求证: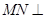 面
面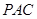 ;
;
(2)探究:是否存在这样的动点M,使得二面角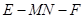 为直二面角?若存在,求CM的长度;若不存在,说明理由.
为直二面角?若存在,求CM的长度;若不存在,说明理由.
已知数列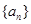 是等比数列,且满足
是等比数列,且满足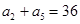 ,
,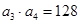 .
.
(1)求数列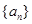 的通项公式;
的通项公式;
(2)若数列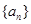 是递增数列,且
是递增数列,且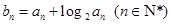 ,求数列
,求数列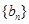 的前n项和
的前n项和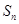 .
.