已知曲线C的极坐标方程为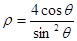 ,直线
,直线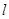 的参数方程为
的参数方程为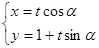 (t为参数,0≤
(t为参数,0≤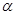 <
< ).
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线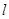 经过点(1,0),求直线
经过点(1,0),求直线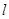 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
(本小题满分8分)某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单 位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
(本小题满分8分)已知命题 函数
函数 在区间
在区间 上是单调递增函数;命题
上是单调递增函数;命题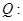 不等式
不等式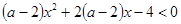 对任意实数
对任意实数 恒成立.若
恒成立.若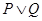 是真命题,求实数
是真命题,求实数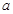 的取值范围.
的取值范围.
已知函数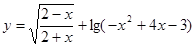 的定义域为
的定义域为 ,
,
(1)求 ;
;
(2)当 时,求函数
时,求函数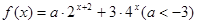 的最小值。
的最小值。
已知函数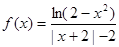
(1)判断 的奇偶性并给予证明;
的奇偶性并给予证明;
(2)求满足 的实数
的实数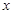 的取值范围。
的取值范围。
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:82,86,87,88,91,94.把这6名学生的得分看成一个总体.
(1)求该总体的平均数与方差;
(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.