已知椭圆C：
的左、右焦点分别为F1、F2，上顶点为A，△AF1F2为正三角形，且以线段F1F2为直径的圆与直线
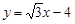相切.
（Ⅰ）求椭圆C的方程和离心率e；
（Ⅱ）若点P为焦点F1关于直线
的对称点，动点M满足
. 问是否存在一个定点T，使得动点M到定点T的距离为定值？若存在，求出定点T的坐标及此定值；若不存在，请说明理由.
已知点M到点
的距离比到点M到直线
的距离小4．
（1）求点M的轨迹C的方程；
（2）若曲线C上存在两点A，B关于直线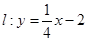
对称，求直线AB的方程．
已知圆M过
，
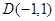两点，且圆心M在
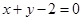上．
（1）求圆M的方程；
（2）设点P是直线
上的动点，PA，PB是圆M的两条切线，A，B为切点，求四边形PAMB面积的最小值．
已知抛物线
，过点
的直线
交C于A，B两点，抛物线C在点A处的切线与在点B处的切线交于点P．
（1）若直线的斜率为1，求
；
（2）求
面积的最小值．
椭圆
的左、右焦点分别是
，过
斜率为1的直线
与椭圆C相交于A，B两点，且
．
（1）求椭圆的离心率；
（2）设点
，
，求椭圆C的方程．
已知函数
，数列
满足
，
，
，e为自然对数的底数．
（1）求函数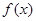
的单调区间；
（2）求证：
．