已知椭圆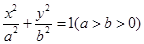 的右焦点为
的右焦点为 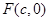 ,
,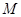 为椭圆的上顶点,
为椭圆的上顶点,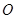 为坐标原点,且两焦点和短轴的两端构成边长为
为坐标原点,且两焦点和短轴的两端构成边长为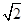 的正方形.
的正方形.
(1)求椭圆的标准方程;
(2)是否存在直线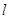 交与椭圆于
交与椭圆于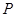 ,
, 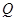 ,且使
,且使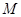 ,使得
,使得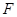 为
为 的垂心,若存在,求出
的垂心,若存在,求出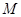 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
(本小题12分)已知函数 的图象在
的图象在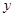 轴上的截距为1,在相邻两最值点
轴上的截距为1,在相邻两最值点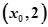 ,
,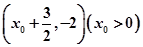 上
上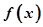 分别取得最大值和最小值.
分别取得最大值和最小值.
⑴求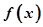 的解析式;
的解析式;
⑵若函数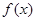 满足方程
满足方程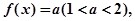 求在
求在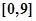 内的所有实数根之和.
内的所有实数根之和.
(本小题满分12分)
设平面向量 = ( m , -1),
= ( m , -1), 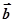 =" (" 2 , n ),其中 m, n
=" (" 2 , n ),其中 m, n {-2,-1,1,2}.
{-2,-1,1,2}.
(1)记“使得 //
//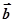 成立的( m,n)”为事件A,求事件A发生的概率;
成立的( m,n)”为事件A,求事件A发生的概率;
(2)记“使得 ⊥(
⊥( -2
-2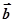 )成立的( m,n)”为事件B,求事件B发生的概率.
)成立的( m,n)”为事件B,求事件B发生的概率.
(本小题满分10分)
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1).
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(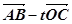 )·
)·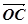 =0,求t的值.
=0,求t的值.
(14分)直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B.
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(14分)设等差数列 满足
满足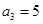 ,
, .
.
(1)求 的通项公式;(2)求
的通项公式;(2)求 的前
的前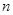 项和
项和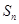 及使得
及使得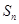 最大的序号
最大的序号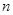 的值.
的值.