数列 满足
满足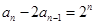
 ,且
,且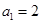 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 若 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:
,求证: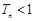 .
.
(本小题满分12分)
已知函数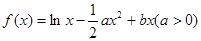 且导数
且导数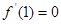 .
.
(1)试用含有 的式子表示
的式子表示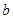 ,并求
,并求 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点 ,且
,且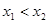 ,如果在函数图像上存在点
,如果在函数图像上存在点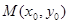 (其中
(其中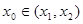 )使得点
)使得点 处的切线
处的切线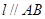 ,则称
,则称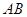 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当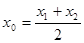 时,又称
时,又称 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数 上是否存在两点
上是否存在两点 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题满分12分)
某学校要对学生进行身体素质全面测试,对每位学生都要进行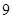 选
选 考核(即共
考核(即共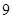 项测试,随机选取
项测试,随机选取 项),若全部合格,则颁发合格证;若不合格,则重新参加下期的
项),若全部合格,则颁发合格证;若不合格,则重新参加下期的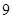 选
选 考核,直至合格为止,若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为
考核,直至合格为止,若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为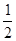 ,第二次参加考试合格的概率为
,第二次参加考试合格的概率为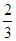 ,第三次参加考试合格的概率为
,第三次参加考试合格的概率为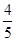 ,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
,若第四次抽到可要求调换项目,其它选项小李均可一次性通过.
(1)求小李第一次考试即通过的概率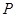 ;
;
(2)求小李参加考核的次数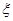 分布列.
分布列.
(本小题满分12分)
设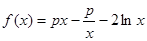 .
.
(1)若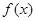 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数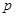 的取值范围;
的取值范围;
(2)设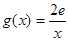 ,且
,且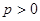 ,若在
,若在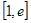 上至少存在一点
上至少存在一点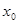 ,使得
,使得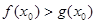 成立,求实数
成立,求实数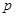 的取值范围.
的取值范围.
(本小题满分12分)
在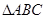 中,若
中,若 ,
,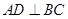 于
于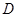 ,则
,则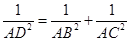 .在四面体
.在四面体 中,若
中,若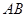 ,
,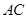 ,
, 两两垂直,
两两垂直, 底面
底面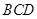 ,垂足为
,垂足为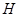 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.
(本小题满分12分)
由下列不等式: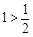 ,
,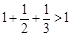 ,
, ,
,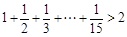 ,
, ,你能得到一个怎样的一般不等式?并加以证明.
,你能得到一个怎样的一般不等式?并加以证明.