已知 、
、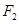 是椭圆
是椭圆
 的左、右焦点,且离心率
的左、右焦点,且离心率 ,点
,点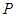 为椭圆上的一个动点,
为椭圆上的一个动点, 的内切圆面积的最大值为
的内切圆面积的最大值为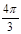 .
.
(1) 求椭圆的方程;
(2) 若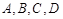 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量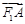 与
与 共线,
共线, 与
与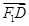 共
共
线,且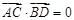 ,求
,求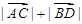 的取值范围.
的取值范围.
(本小题满分12分)已知 分别为
分别为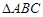 三个内角
三个内角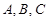 的对边,
的对边, .
.
(1)求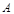 的大小;
的大小;
(2)若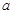 = 7,求
= 7,求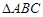 的周长的取值范围.
的周长的取值范围.
若二次函数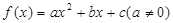 ,满足
,满足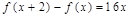 且
且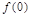 =2.
=2.
(1)求函数 的解析式;
的解析式;
(2)若存在 ,使不等式
,使不等式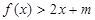 成立,求实数m的取值范围.
成立,求实数m的取值范围.
正方形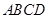 所在平面与平面四边形
所在平面与平面四边形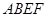 所在平面互相垂直,△
所在平面互相垂直,△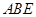 是等腰直角三角形,
是等腰直角三角形,
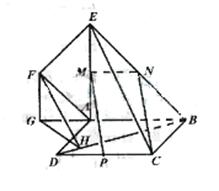
(1)求证: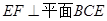 ;
;
(2)设线段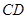 的中点为
的中点为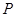 ,在直线
,在直线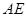 上是否存在一点
上是否存在一点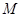 ,使得
,使得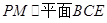 ?若存在,请指出点
?若存在,请指出点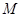 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值.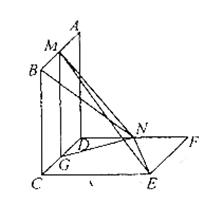
已知奇函数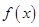 在定义域
在定义域 上单调递减,求满足
上单调递减,求满足 的实数
的实数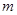 的取值范围.
的取值范围.