(本题9分)如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.

(1)直接写出∠NDE的度数;
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由;


(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD= ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.

如图,在三棱拄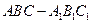 中,
中,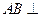 侧面
侧面 ,
,
已知

(Ⅰ)试在棱 (不包含端点
(不包含端点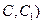 上确定一点
上确定一点 的位置,使得
的位置,使得 ;
; (Ⅱ) 在(Ⅰ)的条件下,求二面角
(Ⅱ) 在(Ⅰ)的条件下,求二面角 的平面角的正切值.
的平面角的正切值.
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(Ⅰ)求这箱产品被用户接收的概率;
(Ⅱ)记抽检的产品件数为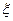 ,求
,求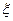 的分布列和数学期望.
的分布列和数学期望.
在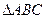 中,
中,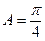 ,
,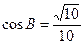 .
.
(Ⅰ)求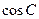 ;
;
(Ⅱ)设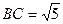 ,求
,求 的值.
的值.
定义: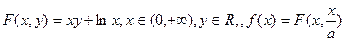 (其中
(其中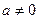 )。
)。
(1)求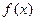 的单调区间;
的单调区间;
(2)若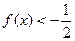 恒成立,试求实数
恒成立,试求实数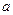 的取值范围;
的取值范围;
若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足
(1)求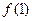 的值;
的值;
(2)若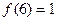 ,解不等式
,解不等式