已知函数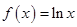 ,
, ,
, (1)若
(1)若 ,求函数
,求函数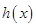 的极值;
的极值;
(2)若函数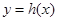 在
在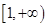 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(3)在函数 的图象上是否存在不同的两点
的图象上是否存在不同的两点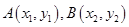 ,使线段
,使线段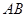 的中点的横坐标
的中点的横坐标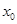 与直线
与直线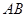 的斜率
的斜率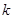 之间满足
之间满足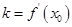 ?若存在,求出
?若存在,求出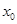 ;若不存在,请说明理由.
;若不存在,请说明理由.
在 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
.
(1)求角 ;
;
(2)若 ,求
,求 的周长
的周长 的取值范围.
的取值范围.
(1)已知 ,
,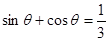 ,求
,求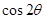 的值;
的值;
(2)已知 ,
,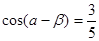 ,
,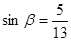 ,求
,求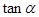 的值.
的值.
近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费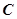 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积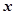 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是 为常数).记
为常数).记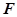 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释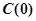 的实际意义,并建立
的实际意义,并建立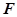 关于
关于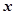 的函数关系式;
的函数关系式;
(2)当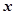 为多少平方米时,
为多少平方米时,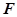 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
已知二次函数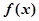 满足:①在
满足:①在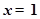 时有极值;②图像过点
时有极值;②图像过点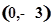 ,且在该点处的切线与直线
,且在该点处的切线与直线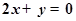 平行.
平行.
(1)求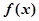 的解析式;
的解析式;
(2)求函数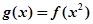 的单调递增区间.
的单调递增区间.
对于函数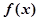 若存在
若存在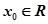 ,
,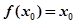 成立,则称
成立,则称 为
为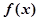 的不动点.已知
的不动点.已知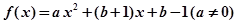
(1)当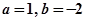 时,求函数
时,求函数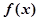 的不动点;
的不动点;
(2)若对任意实数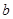 ,函数
,函数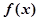 恒有两个相异的不动点,求
恒有两个相异的不动点,求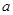 的取值范围.
的取值范围.