(本小题满分12分)
在△ABC中,内角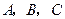 对边的边长分别是
对边的边长分别是 ,已知
,已知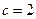 ,
, .
.
(1)若△ABC的面积等于 ,求
,求 ;
;
(2)若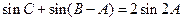 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分12分)
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
(1)估计这所学校成绩在90~140分之间学生的参赛人数;
(2)估计参赛学生成绩的中位数;
(3)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶学习小组.若选出的两人成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.
(本小题满分10分)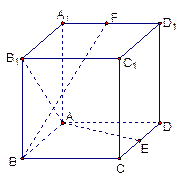
在正方体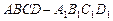 中,E,F分别是CD,A1D1中点
中,E,F分别是CD,A1D1中点
(1)求证:AB1⊥BF;
(2)求证:AE⊥BF;
(3)棱CC1上是否存在点P,使BF⊥平面AEP,若存在,
确定点P的位置;若不存在,说明理由
(本小题共13分)
已知数列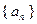 是首项为
是首项为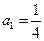 ,公比
,公比 的等比数列.设
的等比数列.设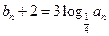
 ,数列
,数列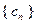 满足
满足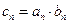 .
.
(Ⅰ)求证:数列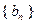 成等差数列;
成等差数列;
(Ⅱ)求数列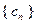 的前
的前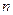 项和
项和 ;
;
(Ⅲ)若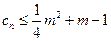 对一切正整数
对一切正整数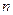 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题共14分)
已知椭圆的中心在坐标原点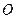 ,长轴长为
,长轴长为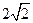 ,离心率
,离心率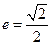 ,过右焦点
,过右焦点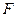 的直线
的直线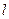 交椭圆于
交椭圆于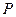 ,
,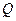 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)当直线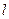 的斜率为1时,求
的斜率为1时,求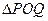 的面积;
的面积;
(Ⅲ)若以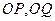 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线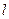 的方程.
的方程.