如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2, .
. 
(1)求证:CD⊥平面PAC;
(2)求二面角M-AB-C的大小;
(3)如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为 ,求
,求 的值.
的值.
已知函数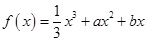
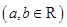 .
.
(1)若曲线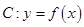 经过点
经过点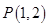 ,曲线
,曲线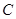 在点
在点 处的切线与直线
处的切线与直线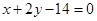 垂直,求
垂直,求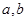 的值;
的值;
(2)在(1)的条件下,试求函数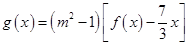 (
(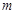 为实常数,
为实常数,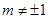 )的极大值与极小值之差;
)的极大值与极小值之差;
(3)若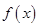 在区间
在区间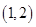 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: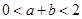 .
.
设 ,
,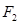 分别是椭圆
分别是椭圆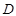 :
: 的左、右焦点,过
的左、右焦点,过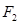 作倾斜角为
作倾斜角为 的直线交椭圆
的直线交椭圆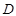 于
于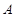 ,
,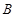 两点,
两点,  到直线
到直线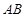 的距离为
的距离为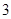 ,连结椭圆
,连结椭圆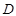 的四个顶点得到的菱形面积为
的四个顶点得到的菱形面积为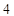 .
.
(1)求椭圆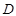 的方程;
的方程;
(2)过椭圆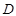 的左顶点
的左顶点 作直线
作直线 交椭圆
交椭圆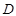 于另一点
于另一点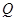 , 若点
, 若点 是线段
是线段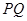 垂直平分线上的一点,且满足
垂直平分线上的一点,且满足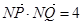 ,求实数
,求实数 的值.
的值.
已知集合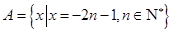 ,
,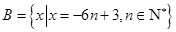 ,设
,设 是等差数列
是等差数列 的前
的前 项和,若
项和,若 的任一项
的任一项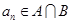 ,且首项
,且首项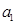 是
是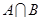 中的最大数,
中的最大数, 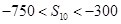 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求
,求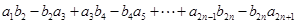 的值.
的值.
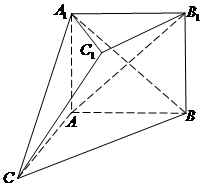
如图,在多面体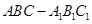 中,四边形
中,四边形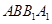 是正方形,
是正方形,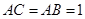 ,
,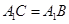 ,
, ,
,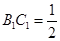
 .
.
(1)求证:面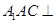 面
面 ;
;
(2)求证: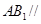 面
面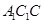 .
.
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
(1)求z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数 .记这8辆轿车的得分的平均数为
.记这8辆轿车的得分的平均数为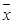 ,定义事件
,定义事件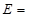 {
{ ,且函数
,且函数 没有零点},求事件
没有零点},求事件 发生的概率.
发生的概率.