解下列方程
(1)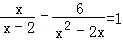
(2)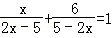 .
.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
解方程: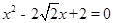
如图,梯形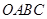 中,
中, 在
在 轴上,
轴上, ∥
∥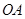 ,∠
,∠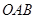 =
=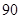 °,
°,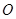 为坐标原点,
为坐标原点, ,
, ,动点
,动点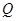 从点
从点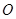 出发,以每秒1个单位的速度沿线段
出发,以每秒1个单位的速度沿线段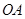 运动,到点
运动,到点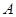 停止,过点
停止,过点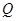 作
作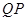 ⊥
⊥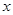 轴交
轴交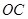 或
或 于点
于点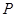 ,以
,以 为一边向右作正方形
为一边向右作正方形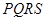 ,设运动时间为
,设运动时间为 (秒),正方形
(秒),正方形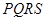 与梯形
与梯形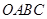 重叠面积为
重叠面积为 (平方单位).
(平方单位).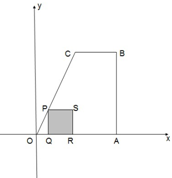
(1)求tan∠AOC.
(2)求 与t的函数关系式.
与t的函数关系式.
(3)求(2)中的 的最大值.
的最大值.
(4)连接 ,
, 的中点为
的中点为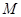 ,请直接写出在正方形
,请直接写出在正方形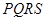 变化过程中,t为何值时,△
变化过程中,t为何值时,△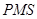 为等腰三角形.
为等腰三角形.
如图,在平面直角坐标系中,四边形 的顶点O为坐标原点,点C在x轴的正半轴上,且
的顶点O为坐标原点,点C在x轴的正半轴上,且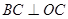 于点
于点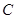 ,点
,点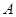 的坐标为(2,2
的坐标为(2,2 ),
), =
=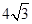 ,
,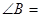 60°,点
60°,点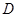 是线段
是线段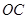 上一点,且
上一点,且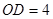 ,连接
,连接 .
.
(1)求证:△AOD是等边三角形;
(2)求点 的坐标;
的坐标;
(3)平行于 的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形
的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形 截得的线段长为
截得的线段长为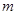 ,直线l与x轴交点的横坐标为t.
,直线l与x轴交点的横坐标为t.
① 当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围).
② 若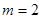 ,请直接写出此时
,请直接写出此时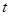 的值.
的值.
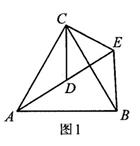
探究:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
结论:(1)∠AEB的度数为;
(2)线段AD、BE之间的数量关系是.
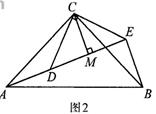
应用:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.