如图，已知：△ABC为边长是的等边三角形，四边形DEFG为边-优题课

如图，已知：△ABC为边长是的等边三角形，四边形DEFG为边长是6的正方形．现将等边△ABC和正方形DEFG按如图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，△ABC从图1的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点C与点F重合时暂停运动，设△ABC的运动时间为t秒（t≥0）．

（1）在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，请直接写出S与t之间的函数关系式；
（2）如图2，当点A与点D重合时，作∠ABE的角平分线BM交AE于M点，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN．在线段AG上是否存在H点，使得△ANH为等腰三角形．如果存在，请求出线段EH的长度；若不存在，请说明理由．
（3）如图3，若四边形DEFG为边长为的正方形，△ABC的移动速度为每秒个单位长度，其余条件保持不变．△ABC开始移动的同时，Q点从F点开始，沿折线FG﹣GD以每秒个单位长度开始移动，△ABC停止运动时，Q点也停止运动．设在运动过程中，DE交折线BA﹣AC于P点，则是否存在t的值，使得PC⊥EQ，若存在，请求出t的值；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

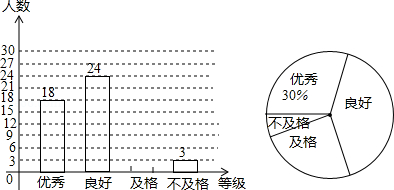
为了贯彻落实健康第一的指导思想，促进学生全面发展，国家每年都要对中学生进行一次体能测试，测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级，某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析，并根据收集的数据绘制了两幅不完整的统计图，请根据这两幅统计图中的信息回答下列问题

（1）本次抽样调查共抽取多少名学生？

（2）补全条形统计图．

（3）在扇形统计图中，求测试结果为“良好”等级所对应圆心角的度数．

（4）若该学校七年级共有600名学生，请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名？

（5）请你对“不及格”等级的同学提一个友善的建议（一句话即可）．

据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过 $15 m / s$ ，在一条笔直公路 $BD$ 的上方 $A$ 处有一探测仪，如平面几何图， $AD = 24 m$ ， $∠ D = 90 °$ ，第一次探测到一辆轿车从 $B$ 点匀速向 $D$ 点行驶，测得 $∠ ABD = 31 °$ ，2秒后到达 $C$ 点，测得 $∠ ACD = 50 ° (\tan 31 ° \approx 0.6$ ， $\tan 50 ° \approx 1.2$ ，结果精确到 $1 m)$

（1）求 $B$ ， $C$ 的距离．

（2）通过计算，判断此轿车是否超速．

在 $ΔABC$ 中， $BC = a$ ， $AC = b$ ， $AB = c$ ，若 $∠ C = 90 °$ ，如图1，则有 $a^{2} + b^{2} = c^{2}$ ；若 $ΔABC$ 为锐角三角形时，小明猜想： $a^{2} + b^{2} > c^{2}$ ，理由如下：如图2，过点 $A$ 作 $AD ⊥ CB$ 于点 $D$ ，设 $CD = x$ ．在 $Rt Δ ADC$ 中， $A D^{2} = b^{2} - x^{2}$ ，在 $Rt Δ ADB$ 中， $A D^{2} = c^{2} - {(a - x)}^{2}$

$∴ a^{2} + b^{2} = c^{2} + 2 ax$

$∵ a > 0$ ， $x > 0$

$∴ 2 ax > 0$

$∴ a^{2} + b^{2} > c^{2}$

$∴$ 当 $ΔABC$ 为锐角三角形时， $a^{2} + b^{2} > c^{2}$

所以小明的猜想是正确的．

（1）请你猜想，当 $ΔABC$ 为钝角三角形时， $a^{2} + b^{2}$ 与 $c^{2}$ 的大小关系．

（2）温馨提示：在图3中，作 $BC$ 边上的高．

（3）证明你猜想的结论是否正确．

甲队修路500米与乙队修路800米所用天数相同，乙队比甲队每天多修30米，问甲队每天修路多少米？

解：设甲队每天修路 $x$ 米，用含 $x$ 的代数式完成表格：

甲队每天修路长度（单位：米）	乙队每天修路长度（单位：米）	甲队修500米所用天数（单位：天）	乙队修800米所用天数（单位：天）
$x$		$\frac{500}{x}$

关系式：甲队修500米所用天数 $=$ 乙队修800米所用天数

根据关系式列方程为：　　

解得：　　

检验：　　

答：　　．

为确保信息安全，在传输时往往需加密，发送方发出一组密码 $a$ ， $b$ ， $c$ 时，则接收方对应收到的密码为 $A$ ， $B$ ， $C$ ．双方约定： $A = 2 a - b$ ， $B = 2 b$ ， $C = b + c$ ，例如发出1，2，3，则收到0，4，5

（1）当发送方发出一组密码为2，3，5时，则接收方收到的密码是多少？

（2）当接收方收到一组密码2，8，11时，则发送方发出的密码是多少？