据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过 ,在一条笔直公路 的上方 处有一探测仪,如平面几何图, , ,第一次探测到一辆轿车从 点匀速向 点行驶,测得 ,2秒后到达 点,测得 , ,结果精确到
(1)求 , 的距离.
(2)通过计算,判断此轿车是否超速.

已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°- ∠FCM.
如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.求证:∠EBF=∠FDE.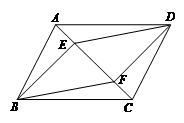
求证:有一组对边平行,和一组对角相等的四边形是平行四边形.(请画出图形,写出已知、求证并证明)
2010年春季我国西南五省持续干旱,旱情牵动着全国人民的心。“一方有难、八方支援”,某厂计划生产1800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务.求原计划每天生产多少吨纯净水?
先化简,再求值: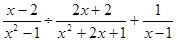 ,其中
,其中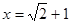 .
.