某中学举行了一次“环保知识竞赛”， 全校学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图
所示）解决下列问题：
频率分布表
| 组别 |
分组 |
频数 |
频率 |
| 第1组 |
[50，60） |
8 |
0.16 |
| 第2组 |
[60，70） |
a |
▓ |
| 第3组 |
[70，80） |
20 |
0.40 |
| 第4组 |
[80，90） |
▓ |
0.08 |
| 第5组 |
[90，100] |
2 |
b |
| |
合计 |
▓ |
▓ |
频率分布直方图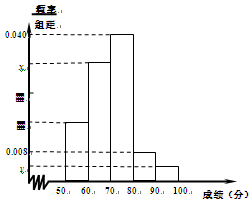
（Ⅰ）写出
的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.求所抽取的2名同学中至少有1名同学来自第5组的概率；
给定两个命题：
：对任意实数
都有
恒成立；
：关于的方程
有实数根；如果与中有且仅有一个为真命题，求实数
的取值范围．
一个袋子中装有质地均匀且完全相同的6个小球，其中黑球、白球各3个，
（1）从袋子中一次任取3个球，求3个小球颜色相同的概率；
（2）若取到1个黑球得1分，取到1个白球得2分，从袋子中取出1个小球记下得分后放入袋中，连续取球三次，求得分之和不小于4的概率.
已知
数列
的前n项和为
，点
在曲线
上
且
.
（1）求数列的通项公式；
（2）数列
的前n项和为且
满足
，试确定
的值，使得数列是等差数列；
（3）求证：
.
设
表示的区域为A，
（1）在区域A中任取一点（x，y），求
的取值范围；
（2）平面上有一定点O（3，3），若一动点M满足
，求点M落入区域A内的概率。
本地一公司计划2011年在省、市两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，省、市电视台的广告收费标准分别为
元/分钟和200元/分钟，规定省、市两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元．问该公司如何分配在省、市两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？