已知平面向量
 若函数
若函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图象上的所有的点向左平移1个单位长度,得到函数
的图象上的所有的点向左平移1个单位长度,得到函数 的图象,若函数
的图象,若函数 在
在 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
设函数

 .
.
(1)当 时,解关于
时,解关于 的不等式
的不等式 ;
;
(2)如果 ,
, ,求
,求 的取值范围.
的取值范围.
已知圆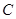 经过点
经过点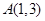 、
、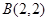 ,并且直线
,并且直线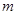 :
: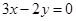 平分圆
平分圆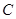 .
.
(Ⅰ)求圆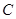 的方程;
的方程;
(Ⅱ)若过点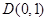 ,且斜率为
,且斜率为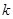 的直线
的直线 与圆
与圆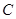 有两个不同的交点
有两个不同的交点 .
.
(ⅰ)求实数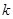 的取值范围;
的取值范围;
(ⅱ)若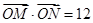 ,求
,求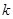 的值.
的值.
设两个向量 、
、 ,满足
,满足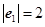 ,
,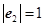 ,
, 、
、 的夹角为
的夹角为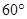 ,若向量
,若向量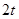
 与向量
与向量
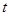
 的夹角为钝角,求实数
的夹角为钝角,求实数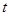 的取值范围.
的取值范围.
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为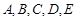 五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为
五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为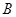 的考生有
的考生有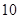 人.
人.
(Ⅰ)求该考场考生中“阅读与表达”科目中成绩为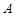 的人数;
的人数;
(Ⅱ)若等级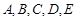 分别对应
分别对应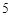 分,
分,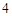 分,
分,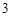 分,
分,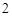 分,
分,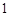 分,求该考场考生“数学与逻辑”科目的平均分;
分,求该考场考生“数学与逻辑”科目的平均分;
(Ⅲ)已知参加本考场测试的考生中,恰有两人的两科成绩均为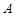 .在至少一科成绩为
.在至少一科成绩为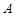 的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为
的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为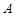 的概率.
的概率.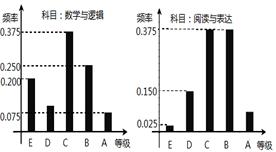
甲、乙、丙三人中要选一人去参加唱歌比赛,于是他们制定了一个规则,规则为:(如图)以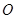 为起点,再从
为起点,再从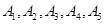 ,这
,这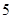 个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为 ,若
,若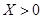 就让甲去;若
就让甲去;若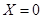 就让乙去;若
就让乙去;若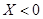 就是丙去.
就是丙去.
(Ⅰ)写出数量积 的所有可能取值;
的所有可能取值;
(Ⅱ)求甲、乙、丙三人去参加比赛的概率,并由求出的概率来说明这个规则公平吗?