(本小题满分14 分)设 ,
, 分别为椭圆
分别为椭圆 :
: 的左、右焦点,点
的左、右焦点,点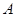 为椭圆
为椭圆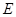 的左顶点,点
的左顶点,点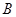 为椭圆
为椭圆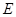 的上顶点,且
的上顶点,且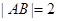 .
.
(1)若椭圆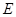 的离心率为
的离心率为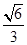 ,求椭圆
,求椭圆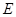 的方程;
的方程;
(2)设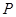 为椭圆
为椭圆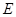 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线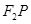 与
与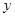 轴相交于点
轴相交于点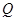 ,若以
,若以 为直径的圆经过点
为直径的圆经过点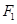 ,证明:点
,证明:点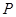 在直线
在直线 上.
上.
如图,直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,∠ACB=900,AC=1,C点到AB1的距离为CE=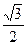 ,D为AB的中点.
,D为AB的中点.
(1)求证:AB1⊥平面CED;
(2)求异面直线AB1与CD之间的距离;
(3)求二面角B1—AC—B的平面角.
如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a,DC=a,F、G分别为EB和AB的中点.
(1)求证:FD∥平面ABC;
(2)求证:AF⊥BD;
(3) 求二面角B—FC—G的正切值.
已知三棱锥P—ABC中,PC⊥底面ABC,AB=BC,
D、F分别为AC、PC的中点,DE⊥AP于E.
(1)求证:AP⊥平面BDE;
(2)求证:平面BDE⊥平面BDF;
(3)若AE∶EP=1∶2,求截面BEF分三棱锥
P—ABC所成两部分的体积比.
在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的,并且这三个四边形也全等,如图①.若用剩下的部分折成一个无盖的正三棱柱形容器,如图②.则当容器的高为多少时,可使这个容器的容积最大,并求出容积的最大值.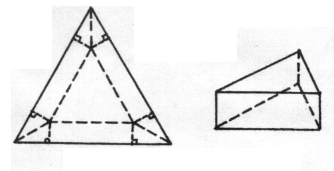
图①图②
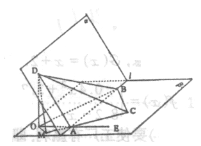
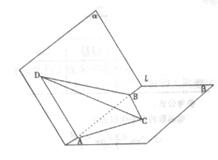
如图a—l—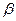 是120°的二面角,A,B两点在棱上,AB=2,D在
是120°的二面角,A,B两点在棱上,AB=2,D在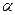 内,三角形ABD是等腰直角三角形,∠DAB=90°,C在
内,三角形ABD是等腰直角三角形,∠DAB=90°,C在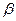 内,
内,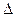 ABC是等腰直角三角形∠ACB=
ABC是等腰直角三角形∠ACB=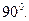
(I)求三棱锥D—ABC的体积;
(2)求二面角D—AC—B的大小;
(3)求异面直线AB、CD所成的角.