身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,抛物线与 轴交于 , 两点,与 轴交于点 ,点 的坐标是 , 为抛物线上的一个动点,过点 作 轴于点 ,交直线 于点 ,抛物线的对称轴是直线 .
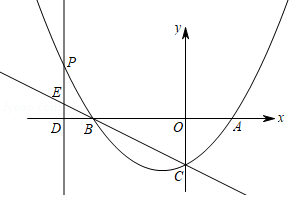
(1)求抛物线的函数表达式;
(2)若点 在第二象限内,且 ,求 的面积.
(3)在(2)的条件下,若 为直线 上一点,在 轴的上方,是否存在点 ,使 是以 为腰的等腰三角形?若存在,求出点 的坐标;若不存在,请说明理由.
如图, 和 是有公共顶点的等腰直角三角形, .
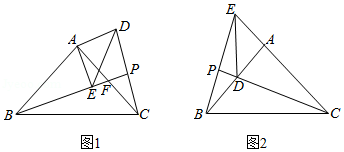
(1)如图1,连接 , , 的延长线交 于点 ,交 于点 ,求证: ;
(2)如图2,把 绕点 顺时针旋转,当点 落在 上时,连接 , , 的延长线交 于点 ,若 , ,求 的面积.
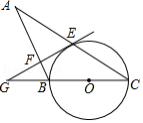
如图, 是 的直径, 是 的弦,过点 作 的切线,交 的延长线于点 ,过点 作 于点 ,交 的延长线于点 .
(1)求证: ;
(2)若 , ,求 的半径.
4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟 分享”比赛活动根据参赛学生的成绩划分为 , , , 四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
|
频数 |
频率 |
|
|
|
4 |
|
|
|
||
|
|
|
0.3 |
|
|
16 |
|
(1)求 , 的值;
(2)求 等级对应扇形圆心角的度数;
(3)学校要从 等级的学生中随机选取2人参加市级比赛,求 等级中的学生小明被选中参加市级比赛的概率.

如图, 中,顶点 的坐标是 , 轴, 交 轴于点 ,顶点 的纵坐标是 , 的面积是24.反比例函数 的图象经过点 和 ,求:
(1)反比例函数的表达式;
(2) 所在直线的函数表达式.
