设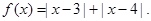
(Ⅰ)求函数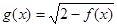 的定义域;
的定义域;
(Ⅱ)若存在实数 满足
满足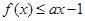 ,试求实数
,试求实数 的取值范围.
的取值范围.
数列{an}(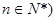 中,a1=1,点(an,an+1)在直线
中,a1=1,点(an,an+1)在直线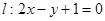 上;
上;
(1)设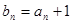 ,求证数列{bn}是等比数列;
,求证数列{bn}是等比数列;
(2)设 ,求{cn}的通项公式;
,求{cn}的通项公式;
求与椭圆 有共同焦点,且过点
有共同焦点,且过点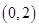 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
在△ABC中,已知角A、B、C所对的三条边分别是a、b、c且满足b2=ac.
求证:0<B≤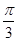 ;(2)求函数y=
;(2)求函数y=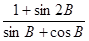 的值域.
的值域.
已知抛物线D的顶点是椭圆Q: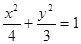 的中心O,焦点与椭圆Q的右焦点重合,点
的中心O,焦点与椭圆Q的右焦点重合,点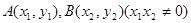 是抛物线D上的两个动点,且
是抛物线D上的两个动点,且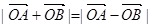
(1)求抛物线D的方程及y1y2的值;
(2)求线段AB中点轨迹E的方程;
(3)在曲线E上寻找一点,使得该点与直线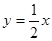 的距离最近.
的距离最近.
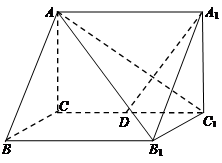
如图所示,在直三棱柱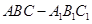 中,
中, ,
,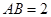 ,
,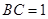 ,
, ,
, 是棱
是棱 的中点.
的中点.
(1)证明: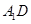
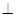 平面
平面 ;
;
(2)求二面角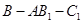 的余弦值.
的余弦值.