定义域为 的函数
的函数 ,其导函数为
,其导函数为 .若对
.若对 ,均有
,均有 ,则称函数
,则称函数 为
为 上的梦想函数.
上的梦想函数.
(Ⅰ)已知函数 ,试判断
,试判断 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;
(Ⅱ)已知函数 (
( ,
, )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 的取值范围;
的取值范围;
(Ⅲ)已知函数 (
( ,
, )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求 的最大整数值.
的最大整数值.
(本小题满分12分)已知椭圆 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.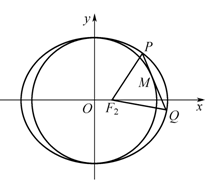
(1)求椭圆的方程;
(2)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于 ,
, 两点,求证:△
两点,求证:△ 的周长是定值.
的周长是定值.
(本小题满分12分)正 的边长为4,
的边长为4, 是
是 边上的高,
边上的高, 、
、 分别是
分别是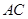 和
和 边的中点,现将
边的中点,现将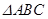 沿
沿 翻折成直二面角
翻折成直二面角 .
.
(Ⅰ)试判断直线 与平面
与平面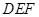 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)求二面角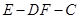 的余弦值;
的余弦值;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使
,使 ?证明你的结论.
?证明你的结论.
(本小题满分12分)为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
| 处罚金额x(单位:元) |
0 |
5 |
10 |
15 |
20 |
| 会闯红灯的人数y |
80 |
50 |
40 |
20 |
10 |
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
①求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
(本小题满分12分)四边形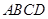 的内角
的内角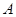 与内角
与内角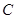 互补,
互补,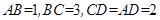 .
.
(Ⅰ)求角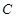 的大小及线段
的大小及线段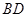 长;
长;
(Ⅱ)求四边形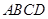 的面积.
的面积.
(本小题满分12分)已知椭圆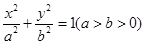 的离心率为
的离心率为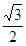 ,且过点
,且过点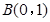 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)直线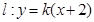 交椭圆于P、Q两点,若点B始终在以PQ为直径的圆内,求实数
交椭圆于P、Q两点,若点B始终在以PQ为直径的圆内,求实数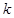 的取值范围.
的取值范围.