已知椭圆C: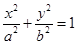 的离心率等于
的离心率等于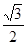 ,点P
,点P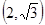 在椭圆上。
在椭圆上。
(1)求椭圆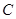 的方程;
的方程;
(2)设椭圆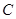 的左右顶点分别为
的左右顶点分别为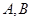 ,过点
,过点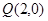 的动直线
的动直线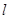 与椭圆
与椭圆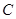 相交于
相交于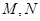 两点,是否存在定直线
两点,是否存在定直线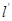 :
: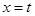 ,使得
,使得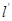 与
与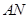 的交点
的交点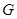 总在直线
总在直线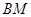 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的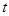 值;若不存在,说明理由.
值;若不存在,说明理由.
(本小题满分12分)
已知A、B、C是 的三个内角,向量
的三个内角,向量 且
且
(1)求角A;
(2)若 ,求
,求 。
。
(本小题满分10分)
已知数列 的前n项和
的前n项和 满足
满足 ,求通项公式
,求通项公式 。
。
已知函数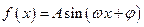
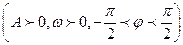 一个周期的图像如图所示。
一个周期的图像如图所示。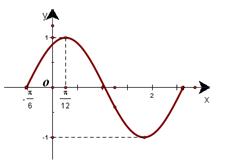
(1)求函数 的表达式;
的表达式;
|
(2)若
 ,且
,且 为
为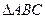 的
的
 的值。
的值。
沪杭高速公路全长166千米,假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州。已知该汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度 (千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(千米/时)的平方成正比,比例系数为0.02;固定部分为200元。
(1)把全程运输成本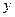 (元)表示为速度
(元)表示为速度 (千
(千 米/时)的函数,并指出这个函数的定义域;
米/时)的函数,并指出这个函数的定义域;
(2)汽车应以多大速度行驶才能使全程运输成本最小?最小运输成本为多少元?
已知函数
(1)求曲线 在点
在点 处的切线的方程;
处的切线的方程;
(2)直线 为曲线
为曲线 的切线,且经过原点,求直线
的切线,且经过原点,求直线 的方程及切点坐标。
的方程及切点坐标。