如图,在平面直角坐标系中,点A、B在x轴上,点C、D在y轴上,且OB=OC=3,OA=OD=1,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,直线AD与抛物线交于另一点M.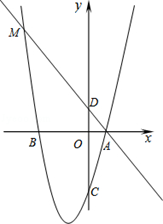
(1)求这条抛物线的解析式;
(2)P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
(3)请直接写出将该抛物线沿射线AD方向平移 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
如图1,在□ABCD中,∠BCD的平分线交直线AD于点F,∠BAD的平分线交DC延长线于E.(1)在图1中,证明AF=EC;
(2)若∠BAD=90°,G为CF的中点(如图2),判断△BEG的形状,并证明.
如图,PA 为⊙O的切线,B、D为⊙O上的两点,如果∠APB=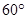 ,∠ADB=
,∠ADB=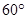 .(1)试判断直线PB与⊙O的位置关系,并说明理由;(2)如果D点是优弧AB上的一个动点,当
.(1)试判断直线PB与⊙O的位置关系,并说明理由;(2)如果D点是优弧AB上的一个动点,当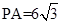 且四边形ADBP是菱形时,求扇形OAMD的面积.
且四边形ADBP是菱形时,求扇形OAMD的面积.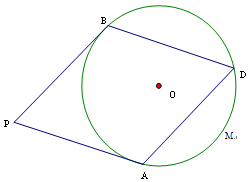
如图,小刚同学在人民广场上观测新华书店楼房墙上的电子屏幕CD, 点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD.(结果保留根号)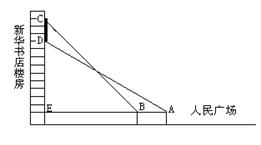
某联欢会上有一个有奖游戏,规则如下:有3张纸牌,背面都是喜羊羊头像,正面有1张是笑脸,其余2张是哭脸.现将3张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是.
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为他得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
今年,某社区响应泰州市政府“爱心一日捐”的号召,积极组织社区居民参加献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.请结合图中相关数据回答下列问题: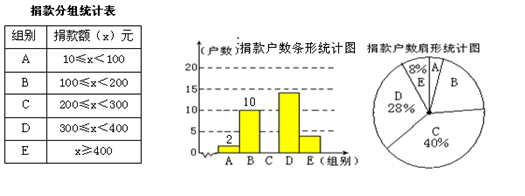
(1)本次调查的样本容量是多少?
(2)求出C组的频数并补全捐款户数条形统计图.
(3)若该社区有1000户住户,请估计捐款不少于200元的户数是多少?