已知函数
, 
．
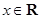（1）求函数
的最大值和最小值；
（2）设函数在
上的图象与
轴的交点从左到右分别为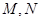
，图象的最高点为
,
求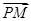
与
的夹角的余弦．
某商场设有会员卡，会员持卡消费都有一定的补贴，商场规定：购买物品不超过100元，补贴5%；购买物品超过100元而不超过5000元，补贴7%；购买物品超过5000元，补贴10%.画出输入消费
元时，输出商场补贴金额
的程序框图.
设计一个计算
值的一个流程图
某教师出了一份共3道题的测试卷，每道题1分。全班的3分、2分、1分和0分的学生所占的比例分别为30%，50%，10%和10%。
（1）若全班共10人，则平均分是多少？
（2）若全班共20人，则平均分是多少？
（3）若该班人数未知，能求出该班的平均分吗？
对于定义域为D的函数
，若同时满足下列条件：①
在D内单调
递增或单调递减；②存在区间[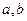
]
，使在[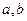]上的值域为[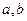]；那么把(
)叫闭函数。
（1）求闭函数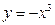
符合条件②的区间[]；
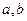（2）判断函数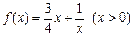
是否为闭函数？并说明理由；
（3）若函数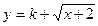
是闭函数，求实数
的取值范围。
已知二次函数
的图像与
轴交于
且有最大值为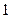
。
（1）求的解析式；
（2）设
，画出
的大致图像，并指出的单调区间；
（3）若方程
恰有四个不同的解，根据图像指出实数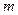
的取值范围。