如图,已知椭圆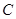 :
: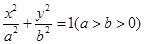 的离心率为
的离心率为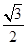 ,以椭圆
,以椭圆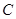 的左顶点
的左顶点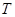 为圆心作圆
为圆心作圆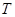 :
: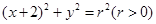 ,设圆
,设圆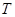 与椭圆
与椭圆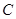 交于点
交于点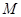 与点
与点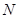 .
.
(1)求椭圆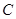 的方程;
的方程;
(2)求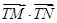 的最小值,并求此时圆
的最小值,并求此时圆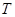 的方程;
的方程;
(3)设点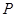 是椭圆
是椭圆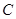 上异于
上异于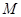 ,
,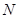 的任意一点,且直线
的任意一点,且直线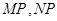 分别与
分别与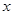 轴交于点
轴交于点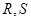 ,
, 为坐标原点,
为坐标原点,
求证: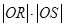 为定值.
为定值.
已知数列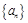 的首项
的首项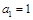 ,前n项之和
,前n项之和 满足关系式:
满足关系式: .
.
(1)求证:数列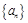 是等比数列;
是等比数列;
(2)设数列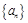 的公比为
的公比为 ,数列
,数列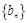 满足
满足 ,且
,且 .
.
(i)求数列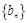 的通项
的通项 ;
;
(ii)设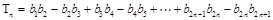 ,求
,求 .
.
咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
已知数列 中,
中, .
.
(1)设 ,求证:数列
,求证:数列 是常数列,并写出其通项公式;
是常数列,并写出其通项公式;
(2)设 ,求证:数列
,求证:数列 是等比数列,并写出其通项公式;
是等比数列,并写出其通项公式;
(3)求数列 的通项公式.
的通项公式.
函数 的图象如图所示.
的图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)已知 ,求
,求 的值.
的值.
△ABC中,AB=AC,M、N分别为AB、AC的中点,且 BN
BN CM,求△ABC的顶角
CM,求△ABC的顶角 的余弦值.
的余弦值.