已知椭圆
的左右焦点分别为
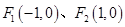，且经过点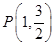
,
为椭圆上的动点，以为圆心，
为半径作圆.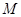
（1）求椭圆
的方程；
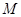（2）若圆与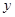
轴有两个交点，求点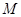横坐标的取值范围.
设函数f(x)=2
在
处取最小值.
(1) 求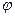
.的值; (2)在
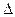ABC中,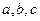
分别是角A,B,C的对边,已知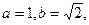
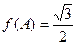,求角C.
（本题14分）函数
，
.
（Ⅰ）求证：函数
的图象关于点
中心对称，并求
的值.
（Ⅱ）设
，
，
，且
，
求证：（ⅰ）当
时，
；（ⅱ）
.
（本小题14分）已知函数
，
（
为常数），若直线
与
和
的图象都相切，且与的图象相切于定点
.（1）求直线的方程及的值；（2）当
时，讨论关于
的方程
的实数解的个数.
求过A(1，2)与B(3，4)两点，且在x轴上截得的弦长等于6的圆的方程．
已知圆x2+y2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b对称，求k、b的值；
若这时两圆的交点为A、B，求∠AOB的度数.