如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= AB.
AB.
(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)求二面角D-A1C-E的正弦值.
已知函数
(1)设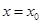 是函数
是函数 的图象的一条对称轴,求
的图象的一条对称轴,求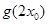 的值;
的值;
(2)求函数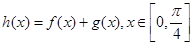 的值域m
的值域m
(本小题满分14分)
已知函数f(x)=2sin2( +x)-
+x)- cos2x.
cos2x.
(1)求f(x)的值域;
(2)求f(x)的周期及单调递减区间.
.(本小题满分14分)
给定两个长度为1的平面向量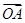 和
和 ,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为120°.如图所示,点C在以O为圆心的圆弧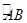 上变动.若
上变动.若 ,其中x,yÎR,试求x+y的最大值.
,其中x,yÎR,试求x+y的最大值.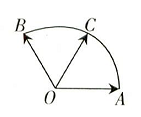
(本小题满分10分)
已知函数y=Asin(wx+j)(A>0,w>0,0<j<p)最大值是2,最小正周期是 ,直线x=0是其图象的一条对称轴,求此函数的解析式.
,直线x=0是其图象的一条对称轴,求此函数的解析式.
.(本小题满分10分)
求(cos220°- )·(1+
)·(1+ tan10°)的值.
tan10°)的值.