(本小题满分14分)已知{an}是等差数列,其前n项的和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=21,S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
设向量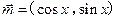 ,
,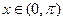 ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)设 ,求函数
,求函数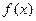 的值域.
的值域.
(1)若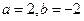 ,求函数
,求函数 的极值;
的极值;
(2)若 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出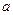 关于
关于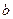 的关系式(用
的关系式(用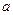 表示
表示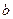 ),并确定
),并确定 的单调区间;
的单调区间;
(3)在(2)的条件下,设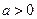 ,函数
,函数 .若存在
.若存在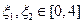 使得
使得 成立,求
成立,求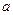 的取值范围.
的取值范围.
已知数列 和
和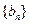 满足
满足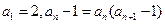 ,
, ,
, .
.
(1)求数列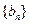 的通项公式;
的通项公式;
(2)设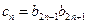 ,求使得
,求使得
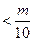 对一切
对一切 都成立的最小正整数
都成立的最小正整数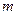 ;
;
(3)设数列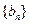 的前
的前 和为
和为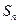 ,
,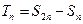 ,试比较
,试比较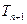 与
与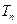 的大小.
的大小.
已知点C(1,0),点A、B是⊙O: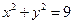 上任意两个不同的点,
上任意两个不同的点,
且满足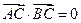 ,设P为弦AB的中点,
,设P为弦AB的中点,
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线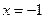 的
的
距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE
为平行四边形,DC 平面ABC ,
平面ABC , ,
, .
.
(1)证明:平面ACD 平面
平面 ;
;
(2)记 ,
, 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求 的表达式;
的表达式;
 (3)当
(3)当 取得最大值时,求证:AD=CE.
取得最大值时,求证:AD=CE.