如图，正方形ABCD的边长是3，点P是直线BC上一点，连接P-优题课

如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF，CF．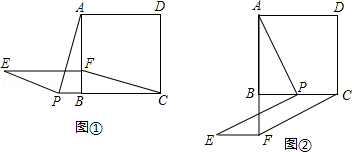

（1）如图①，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；
（2）如图②，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；
（3）在（2）的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由．

科目数学题型解答题难度较难

知识点：圆内接四边形的性质

如图，已知一次函数 $y = kx + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点 $A (3, a)$ ，点 $B (14 - 2 a, 2)$ ．

（1）求反比例函数的表达式；

（2）若一次函数图象与 $y$ 轴交于点 $C$ ，点 $D$ 为点 $C$ 关于原点 $O$ 的对称点，求 $ΔACD$ 的面积．

（1）化简： $(a - 1 + \frac{1}{a - 3}) \div \frac{a^{2} - 4}{a - 3}$ ；

（2）解不等式： $\frac{x + 1}{3} - 1 < \frac{x - 1}{4}$ ．

如图，菱形 $ABCD$ 的边长为1， $∠ ABC = 60 °$ ，点 $E$ 是边 $AB$ 上任意一点（端点除外），线段 $CE$ 的垂直平分线交 $BD$ ， $CE$ 分别于点 $F$ ， $G$ ， $AE$ ， $EF$ 的中点分别为 $M$ ， $N$ ．

（1）求证： $AF = EF$ ；

（2）求 $MN + NG$ 的最小值；

（3）当点 $E$ 在 $AB$ 上运动时， $∠ CEF$ 的大小是否变化？为什么？

已知抛物线 $y = a x^{2} - 2 ax - 3 + 2 a^{2} (a \neq 0)$ ．

（1）求这条抛物线的对称轴；

（2）若该抛物线的顶点在 $x$ 轴上，求其解析式；

（3）设点 $P (m, y_{1})$ ， $Q (3, y_{2})$ 在抛物线上，若 $y_{1} < y_{2}$ ，求 $m$ 的取值范围．

已知 $⊙ O_{1}$ 的半径为 $r_{1}$ ， $⊙ O_{2}$ 的半径为 $r_{2}$ ．以 $O_{1}$ 为圆心，以 $r_{1} + r_{2}$ 的长为半径画弧，再以线段 $O_{1} O_{2}$ 的中点 $P$ 为圆心，以 $\frac{1}{2} O_{1} O_{2}$ 的长为半径画弧，两弧交于点 $A$ ，连接 $O_{1} A$ ， $O_{2} A$ ， $O_{1} A$ 交 $⊙ O_{1}$ 于点 $B$ ，过点 $B$ 作 $O_{2} A$ 的平行线 $BC$ 交 $O_{1} O_{2}$ 于点 $C$ ．

（1）求证： $BC$ 是 $⊙ O_{2}$ 的切线；

（2）若 $r_{1} = 2$ ， $r_{2} = 1$ ， $O_{1} O_{2} = 6$ ，求阴影部分的面积．

试卷网试题网古诗词网作文网范文网