如图，菱形ABCD的边长为1，∠ABC60°，点E是边AB上-优题课

题文

如图，菱形 $ABCD$ 的边长为1， $∠ ABC = 60 °$ ，点 $E$ 是边 $AB$ 上任意一点（端点除外），线段 $CE$ 的垂直平分线交 $BD$ ， $CE$ 分别于点 $F$ ， $G$ ， $AE$ ， $EF$ 的中点分别为 $M$ ， $N$ ．

（1）求证： $AF = EF$ ；

（2）求 $MN + NG$ 的最小值；

（3）当点 $E$ 在 $AB$ 上运动时， $∠ CEF$ 的大小是否变化？为什么？

科目数学题型解答题难度较难

知识点：菱形的性质轴对称-最短路线问题等边三角形的判定与性质三角形中位线定理

登录免费查看答案和解析

相关试题

已知：b是最小的正整数，且a、b满足=0，请回答问题
（1）请直接写出a、b、c的值。
a=__________； b=__________；c=__________
（2）a、b、c所对应的点分别为A、B、C，点P为一动点，其对应的数为x，点P在0到2之间运动时（即0≤x≤2时），请化简式子：（请写出化简过程）

（3）在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动，假设t秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB。请问：BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值。

已知：x₁，x₂，…x₂₀₁₂都是不等于0的有理数，请你探究以下问题：
（1）若y₁=，则= ；
（2）若y₂=，则= ；
（3）若y₃=，则= ；
（4）由以上探究可知，y₂₀₁₂=，共有个不同的值。请求出这些不同的y₂₀₁₂的值的绝对值的和。

奶奶提一篮子玉米到集贸市场去兑换大米，每2kg玉米兑换1kg大米，商贩用秤称得连篮子带玉米恰好20kg，于是商贩连篮子带大米给奶奶共10kg，在这个过程中谁吃亏?吃亏有多大？（设合适的字母，然后用字母表示）

下图是一个数字转换机，请解答下列问题：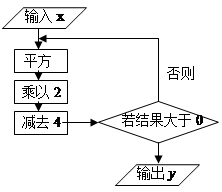

（1）填空：若输入的x值为2，则输出的y值为
（2）若输入的x值为1，则输出的y值为
（3）若输出的y值为28，那么输入的x值是什么？（写出三个x值，并写出简要的分析过程．）

如图，大正方形的边长为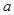，小正方形的边长为b，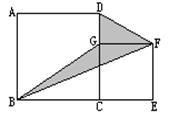

（1）用代数式表示阴影部分的面积；
（2）当a=10，b=4时，求阴影部分的面积．

试卷网试题网古诗词网作文网范文网