先阅读以下材料，然后解答问题：材料：将二次函数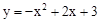的图象向左平移-优题课

先阅读以下材料，然后解答问题：
材料：将二次函数的图象向左平移1个单位，再向下平移2个单位，求平移后的抛物线的解析式（平移后抛物线的形状不变）。
解：在抛物线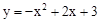上任取两点A（0，3）、B（1，4），由题意知：点A向左平移1个单位得到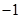（，3），再向下平移2个单位得到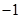（，1）；点B向左平移1个单位得到（0，4），再向下平移2个单位得到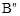（0，2）。
设平移后的抛物线的解析式为。
则点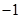（，1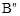），（0，2）在抛物线上。
可得：，解得：。
所以平移后的抛物线的解析式为：。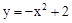
根据以上信息解答下列问题：
将直线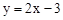向右平移3个单位，再向上平移1个单位，求平移后的直线的解析式。

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

（1）计算： $4 \sin 60 ° + {(π - 2)}^{0} - {(- \frac{1}{2})}^{- 2} - \sqrt{12}$ ．

（2） $x$ 为何值时，两个代数式 $x^{2} + 1$ ， $4 x + 1$ 的值相等？

如图，在 $Rt Δ ABC$ 中， $∠ C = 90 °$ ， $AC = 6$ ， $∠ BAC = 60 °$ ， $AD$ 平分 $∠ BAC$ 交 $BC$ 于点 $D$ ，过点 $D$ 作 $DE / / AC$ 交 $AB$ 于点 $E$ ，点 $M$ 是线段 $AD$ 上的动点，连结 $BM$ 并延长分别交 $DE$ ， $AC$ 于点 $F$ 、 $G$ ．

（1）求 $CD$ 的长．

（2）若点 $M$ 是线段 $AD$ 的中点，求 $\frac{EF}{DF}$ 的值．

（3）请问当 $DM$ 的长满足什么条件时，在线段 $DE$ 上恰好只有一点 $P$ ，使得 $∠ CPG = 60 °$ ？

定义：在平面直角坐标系中，对于任意两点 $A (a, b)$ ， $B (c, d)$ ，若点 $T (x, y)$ 满足 $x = \frac{a + c}{3}$ ， $y = \frac{b + d}{3}$ 那么称点 $T$ 是点 $A$ ， $B$ 的融合点．

例如： $A (- 1, 8)$ ， $B (4, - 2)$ ，当点 $T (x, y)$ 满足 $x = \frac{- 1 + 4}{3} = 1$ ， $y = \frac{8 + (- 2)}{3} = 2$ 时，则点 $T (1, 2)$ 是点 $A$ ， $B$ 的融合点．

（1）已知点 $A (- 1, 5)$ ， $B (7, 7)$ ， $C (2, 4)$ ，请说明其中一个点是另外两个点的融合点．

（2）如图，点 $D (3, 0)$ ，点 $E (t, 2 t + 3)$ 是直线 $l$ 上任意一点，点 $T (x, y)$ 是点 $D$ ， $E$ 的融合点．

①试确定 $y$ 与 $x$ 的关系式．

②若直线 $ET$ 交 $x$ 轴于点 $H$ ．当 $ΔDTH$ 为直角三角形时，求点 $E$ 的坐标．

某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间．经市场调查表明，该馆每间标准房的价格在 $170 ~ 240$ 元之间（含170元，240元）浮动时，每天入住的房间数 $y$ （间 $)$ 与每间标准房的价格 $x$ （元 $)$ 的数据如下表：

$x$ （元 $)$	$\dots$	190	200	210	220	$\dots$
$y$ （间 $)$	$\dots$	65	60	55	50	$\dots$

（1）根据所给数据在坐标系中描出相应的点，并画出图象．

（2）求 $y$ 关于 $x$ 的函数表达式，并写出自变量 $x$ 的取值范围．

（3）设客房的日营业额为 $w$ （元 $)$ ．若不考虑其他因素，问宾馆标准房的价格定为多少元时，客房的日营业额最大？最大为多少元？

如图，在等腰 $ΔABC$ 中， $AB = AC$ ，以 $AC$ 为直径作 $⊙ O$ 交 $BC$ 于点 $D$ ，过点 $D$ 作 $DE ⊥ AB$ ，垂足为 $E$ ．

（1）求证： $DE$ 是 $⊙ O$ 的切线．

（2）若 $DE = \sqrt{3}$ ， $∠ C = 30 °$ ，求 $\hat{AD}$ 的长．