如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．
（1）求直线AB的函数解析式；
（2）当点P在线段AB（不包括A，B两点）上时．
①求证：∠BDE=∠ADP；
②设DE=x，DF=y．请求出y关于x的函数解析式；
（3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．
如图，在平面直角坐标系
中，
，
，
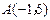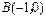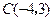．（1）在图中画出
关于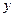
轴的对称图形
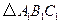；（2）直接写出点
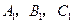的坐标．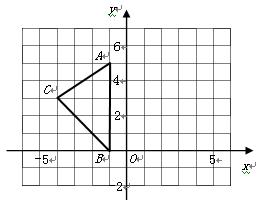
已知：如图，A、C、F、D在同一直线上，AF＝DC，AB＝DE，BC＝EF，
求证：△ABC≌△DEF．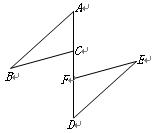
已知：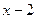
的平方根为
，
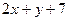的立方根为3，求：
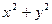的平方根.
（本题10分）如图，在梯形ABCD中，AD//BC，E是BC的中点，AD="5" cm，BC="12" cm，CD=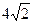
cm，∠C=45°，点P从B点出发，沿着BC方向以1cm/s运动，到达点C停止，设P运动了ts。（1）当t为何值时以点P、A、D、E为顶点的四边形为直角梯形；
（2）当t为何值时以点P、A、D、E为顶点的四边形为平行四边形；
（3）点P在BC边上运动的过程中，以P、A、D、E为顶点的四边形能否构成菱形？如能，请求出t值，如不能请说明理由。
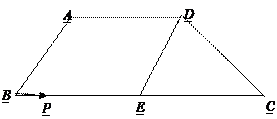
（本题10分） 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点得四边形EFGH．如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；（1）如图2，当四边形ABCD为矩形时，则四边形EFGH的形状是；
（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=
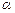（0°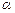＜＜90°），① 试用含
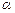的代数式表示∠HAE=；② 求证：HE=HG；③ 四边形EFGH是什么四边形？并说明理由．
