某学校开展课外体育活动，决定开设A：篮球、B：乒乓球、C：踢毽子、D：跑步四种活动项目．为了解学生最喜欢哪一种活动项目（每人只选取一种），随机抽取了部分学生进行调查，并将调查结果绘成如甲、乙所示的统计图，请你结合图中信息解答下列问题．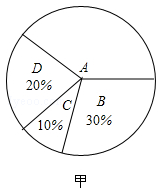
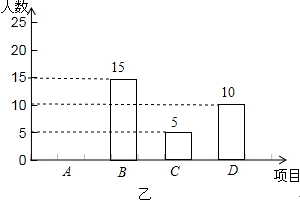
（1）样本中最喜欢A项目的人数所占的百分比为 ，其所在扇形统计图中对应的圆心角度数是 度；
（2）请把条形统计图补充完整；
（3）若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少？
观察下列等式
，
，
，将以这三个等式两边分别相加得：
。
（1）猜想并写出：
_________
（2）直接写出下列各式的计算结果：
_________
（3）探究并计算：
某服装厂生产一种西装和领带，西装每套定价300元，领带每条定价50元。厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90％付款。现某客户要到该服装厂购买西装20套，领带x条（x＞20）。
（1）若该客户按方案①购买，需付款________元（用含x的代数式表示）；
若该客户按方案②购买，需付款________元（用含x的代数式表示）。
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？
观察下列解题过程
计算：
解：设S=① ,则5S=
②
由②－①得：
,∴
你能用你学到的方法计算下面的题吗？
数a，b，c在数轴上的位置如图所示且|a|=|c|；
化简：|a+c|+|2b|﹣|b﹣a|﹣|c﹣b|+|a+b|．
先化简，再求值：
其中