设点A( ,0),B(
,0),B( ,0),直线AM、BM相交于点M,且它们的斜率之积为
,0),直线AM、BM相交于点M,且它们的斜率之积为 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)若直线 过点F(1,0)且绕F旋转,
过点F(1,0)且绕F旋转, 与圆
与圆 相交于P、Q两点,
相交于P、Q两点, 与轨迹C相交于R、S两点,若|PQ|
与轨迹C相交于R、S两点,若|PQ|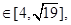 求△
求△ 的面积的最大值和最小值(F′为轨迹C的左焦点).
的面积的最大值和最小值(F′为轨迹C的左焦点).
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,
他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知函数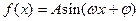
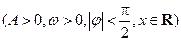 的图象的一部分如下图所示.
的图象的一部分如下图所示.
(1)求函数 的解析式;
的解析式;
(2)当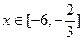 时,求函数
时,求函数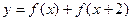 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
已知函数: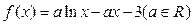
(1)讨论函数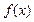 的单调性;
的单调性;
(2)若函数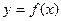 的图像在点
的图像在点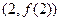 处的切线的倾斜角为
处的切线的倾斜角为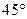 ,问:
,问: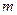 在什么范围取值时,函数
在什么范围取值时,函数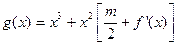 在区间
在区间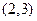 上总存在极值?
上总存在极值?
(3)求证: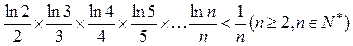 .
.
某地区预计明年从年初开始的前 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量 (万件)与月份
(万件)与月份 的近似关系为
的近似关系为 .
.
(1)写出明年第 个月的需求量
个月的需求量 (万件)与月份
(万件)与月份 的函数关系式,并求出哪个月份的需求量超过1.4万件;
的函数关系式,并求出哪个月份的需求量超过1.4万件;
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件
设函数 .
.
(1)求函数 的最小正周期及其在区间
的最小正周期及其在区间 上的值域;
上的值域;
(2)记 的内角A,B,C的对边分别为
的内角A,B,C的对边分别为 ,若
,若 且
且 ,求角B的值.
,求角B的值.