（本小题满分13分）某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和后期会因供应不足使价格呈持续上涨态势，而中期又将出现供大于求，使价格连续下跌．现有三种价格模拟函数：①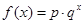
；②
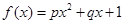；③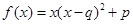
．（以上三式中
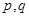均为常数，且
）
（1）为准确研究其价格走势，应选哪种价格模拟函数(不必说明理由)
（2）若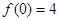
，
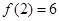，求出所选函数
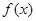的解析式（注：函数定义域是
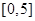．其中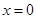
表示8月1日，
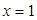表示9月1日，…，以此类推）；
（3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．
已知函数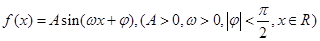
的图像的一部分如图所示.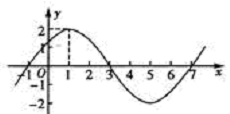
（Ⅰ）求函数
的解析式;
（Ⅱ）求函数
的最值;
已知函数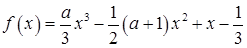
(
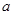
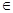R)．
(1)若
，求函数
的极值；
（2）是否存在实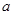数使得函数在区间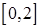
上有两个零点，若存在，求出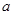的取值范围；若不存在，说明理由。
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周（阴影部分）为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为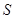
平方米.
（1）分别写出用
表示
和用表示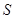的函数关系式（写出函数定义域）；
（2）怎样设计能使S取得最大值，最大值为多少？
如图，棱柱ABCD—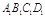
的底面
为菱 形 ，AC∩BD=O侧棱
⊥BD,点F为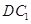
的中点．
（Ⅰ）证明：
平面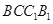
；
（Ⅱ）证明：平面
平面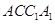
.
已知数列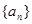
是等差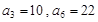数列,
，数列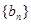
的前n项和是
，且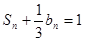
.
（I）求数列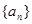的通项公式；
（II）求证：数列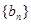是等比数列；