如图,在等腰梯形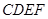 中,
中,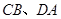 是梯形的高,
是梯形的高,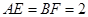 ,
,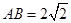 ,现将梯形沿
,现将梯形沿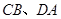 折起,使
折起,使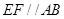 ,且
,且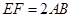 ,得一简单组合体
,得一简单组合体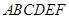 如图所示,已知
如图所示,已知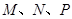 分别为
分别为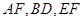 的中点.
的中点.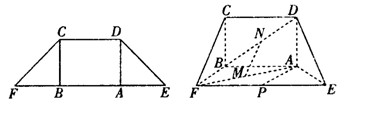
(1)求证: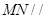 平面
平面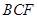 ;
;
(2)求证: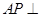 平面
平面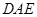 .
.
某研究机构对高中学生的记忆力 和判断力
和判断力 进行统计分析,得下表数据
进行统计分析,得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
(1)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式: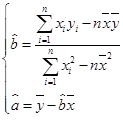
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若 是从集合
是从集合 中任取一个元素,
中任取一个元素, 是从集合
是从集合 中任取一个元素,求方程
中任取一个元素,求方程 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 是从集合
是从集合 中任取一个元素,
中任取一个元素, 是从集合
是从集合 中任取一个元素,求上述方程有实根的概率.
中任取一个元素,求上述方程有实根的概率.
命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ;,命题
;,命题 :函数
:函数 为增函数.如果命题“
为增函数.如果命题“ ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
如图,椭圆 的一个焦点是
的一个焦点是 ,
, 为坐标原点.
为坐标原点.
(1)已知椭圆短轴的两个三等分点 与一个焦点构成正三角形,求椭圆的方程;
与一个焦点构成正三角形,求椭圆的方程;
(2)设过点 的直线
的直线 交椭圆于
交椭圆于 两点.若直线
两点.若直线 绕点
绕点 任意转动,则有
任意转动,则有 ,求
,求 的取值范围.
的取值范围.
已知椭圆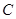 :
: 的右焦点
的右焦点 ,过
,过 的直线交椭圆
的直线交椭圆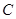 于
于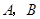 两点,且
两点,且 是线段
是线段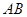 的中点.
的中点.
(1)求椭圆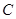 的方程;
的方程;
(2)已知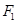 是椭圆的左焦点,求
是椭圆的左焦点,求 的面积.
的面积.