本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知椭圆的中心在坐标原点 ,焦点在
,焦点在 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点 与
与 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于 两点.
两点.
(1)求椭圆的方程;
(2)当直线 的斜率为1时,求
的斜率为1时,求 的面积;
的面积;
(3)在线段 上是否存在点
上是否存在点 ,使得以
,使得以 为邻边的平行四边形是菱形?
为邻边的平行四边形是菱形?
若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分14分)
已知数列 的前n项和为
的前n项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)设数列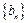 满足:
满足: ,且
,且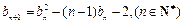 ,
,
求证: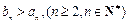 ;
;
(3)求证: 。
。
(本小题满分13分)已知函数 (其中x≥1)
(其中x≥1)
(1)求函数 的反函数
的反函数 ;
;
(2)设 ,求函数
,求函数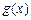 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式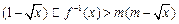 对于区间
对于区间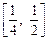 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为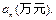
(1)求 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据:
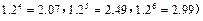
已知数列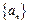 的各项均是正数,其前
的各项均是正数,其前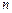 项和为
项和为 ,满足
,满足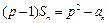 ,其中
,其中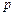 为正常数,且
为正常数,且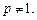
 (1)求数列
(1)求数列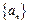 的通项公式;(2)设
的通项公式;(2)设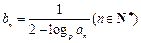 ,数列
,数列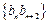 的前
的前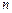 项和为
项和为 ,求证:
,求证: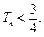
(本小题满分12分)数列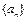 中,
中,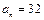 ,
, ,
,
(1)若数列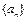 为公差为11的等差数列,求
为公差为11的等差数列,求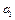 ;
;
(2)若数列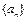 为以
为以 为首项的等比数列,求数列
为首项的等比数列,求数列 的前m项和
的前m项和
