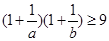本题共有3小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
已知无穷等比数列 公比为
公比为 ,各项的和等于9,数列
,各项的和等于9,数列 各项的和为
各项的和为 .对给定的
.对给定的 ,设
,设 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
(1)求数列 的通项
的通项 ;
;
(2)求数列 的前10项之和;
的前10项之和;
(3)设 为数列
为数列 的第
的第 项,
项, ,求正整数
,求正整数 ,使得
,使得 存在且不等于零.
存在且不等于零.
如图,在侧棱垂直于底面的三棱柱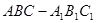 中,
中,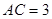 ,
,  ,点
,点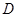 是
是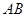 的中点.
的中点.
(1)求证: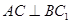 ;
;
(2)求证: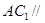 平面
平面 ;
;
(3)求三棱锥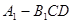 的体积.
的体积.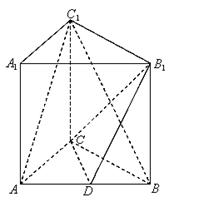
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
| 年份200x(年) |
0 |
1 |
2 |
3 |
4 |
| 人口数y(十)万 |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出Y关于x的线性回归方程Y=bx+a;
(3)据此估计2005年.该 城市人口总数。
观察下列三角形数表假设第n行的第二个数为 (n≥2,n∈N*).
(n≥2,n∈N*).
(Ⅰ)依次写出第六行的所有6个数字;
(Ⅱ)归纳出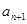 与
与 的关系式并求出
的关系式并求出 的通项公式;
的通项公式;
已知Z是复数,Z+2i, 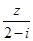 均为实数(i为虚数单位),且复数
均为实数(i为虚数单位),且复数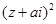 在复平面对应的点在第二象限,求实数a的取值范围.
在复平面对应的点在第二象限,求实数a的取值范围.
已知 ,且
,且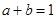 ,求证:
,求证: