(1)若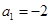 ,点
,点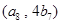 在函数
在函数 的图像上,求数列
的图像上,求数列 的前
的前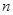 项和
项和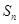 ;
;
(2)若a1=1,函数f(x)的图像在点(a2,b2)处的切线在x轴上的截距为2- ,求数列
,求数列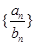 的前n项和Tn.
的前n项和Tn.
如图所示,在平面四边形ABCD中,AD=1,CD=2,AC= .
.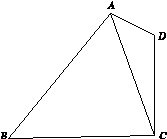
(1)求cos∠CAD的值;
(2)若cos∠BAD= ,sin∠CBA=
,sin∠CBA= ,求BC的长.
,求BC的长.
一条斜率为1的直线 与离心率为
与离心率为 的椭圆
的椭圆 :
: (
( )交于
)交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,且
,且 ,
, ,求直线
,求直线 和椭圆
和椭圆 的方程.
的方程.
已知 ,设命题
,设命题 函数
函数 在R上单调递增;命题
在R上单调递增;命题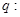 不等式
不等式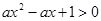 对
对 恒成立。若
恒成立。若 为假,
为假,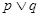 为真,求
为真,求 的取值范围.
的取值范围.
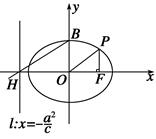
如图,已知 是椭圆
是椭圆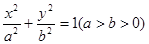 上且位于第一象限的一点,
上且位于第一象限的一点,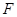 是椭圆的右焦点,
是椭圆的右焦点,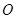 是椭圆的中心,
是椭圆的中心, 是椭圆的上顶点,
是椭圆的上顶点, 是直线
是直线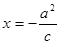 (
( 是椭圆的半焦距)与
是椭圆的半焦距)与 轴的交点,若
轴的交点,若 ,
, ,试求椭圆的离心率的平方的值.
,试求椭圆的离心率的平方的值.