如图,已知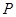 是椭圆
是椭圆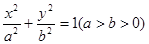 上且位于第一象限的一点,
上且位于第一象限的一点,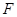 是椭圆的右焦点,
是椭圆的右焦点,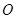 是椭圆的中心,
是椭圆的中心, 是椭圆的上顶点,
是椭圆的上顶点, 是直线
是直线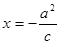 (
( 是椭圆的半焦距)与
是椭圆的半焦距)与 轴的交点,若
轴的交点,若 ,
, ,试求椭圆的离心率的平方的值.
,试求椭圆的离心率的平方的值.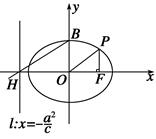
(本小题满分12分)某市为调研高三一轮复习质量在2015年1月份组织了一次期末统一考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: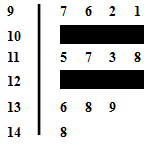
| 分数段 |
 |
 |
 |
| 频数 |
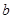 |
||
| 频率 |
 |
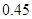 |
(Ⅰ)求表中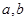 的值并估计这次考试全校学生数学成绩优秀的人数(分数在
的值并估计这次考试全校学生数学成绩优秀的人数(分数在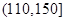 范围为优秀);
范围为优秀);
(Ⅱ)从得分在 内的学生随机选2名学生得分,求2名学生的平均分不低于140分的概率.
内的学生随机选2名学生得分,求2名学生的平均分不低于140分的概率.
(本小题满分12分)在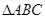 中,角
中,角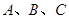 所对的边分别为
所对的边分别为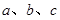 ,且
,且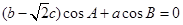 .
.
(Ⅰ)求角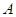 ;
;
(Ⅱ)若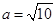 ,
, ,
,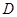 为
为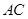 的中点,求
的中点,求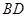 的长度.
的长度.
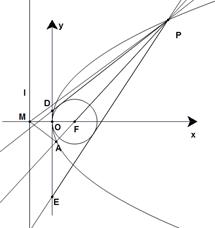
(本小题满分14分)已知抛物线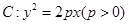 的焦点为
的焦点为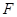 ,准线
,准线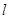 与
与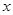 轴的交点为
轴的交点为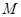 .点
.点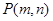 (
( )在抛物线
)在抛物线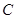 上,且
上,且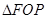 的外接圆圆心到准线
的外接圆圆心到准线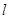 的距离为
的距离为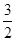 .
.
(Ⅰ)求抛物线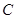 的方程;
的方程;
(Ⅱ)若直线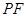 与抛物线
与抛物线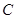 交于另一点
交于另一点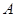 ,证明:
,证明: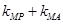 为定值;
为定值;
(Ⅲ)过点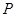 作圆
作圆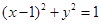 的两条切线,与
的两条切线,与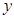 轴分别交于
轴分别交于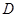 、
、 两点,求
两点,求 面积取得最小值时对应的
面积取得最小值时对应的 值.
值.
(本小题满分13分)已知函数 .
.
(Ⅰ)求函数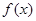 的单调区间;
的单调区间;
(Ⅱ)是否存在实数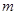 ,使得当
,使得当 时,对任意的
时,对任意的 ,恒有
,恒有 ?若存在,试求出实数
?若存在,试求出实数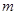 的取值范围,若不存在,试说明理由.
的取值范围,若不存在,试说明理由.
(本小题满分12分) 已知数列 的前
的前 项和为
项和为 ,数列
,数列 是公比为2的等比数列,且
是公比为2的等比数列,且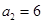 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若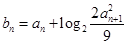 ,数列
,数列 的前
的前 项和为
项和为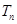 ,求使
,求使 成立的最小正整数
成立的最小正整数 .
.