如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,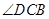 =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO=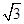 ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2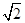 ,
,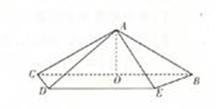
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M且有|PM|=|PO|(O为原点),求使|PM|取得最小值时点P的坐标.
已知关于x的一元二次方程x2﹣2(a﹣2)x﹣b2+16=0
(1)若a,b是一枚骰子掷两次所得到的点数,求方程有两正根的概率.
(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.
(本小题满分10分)选修4—5:不等式选讲
已知a+b=1,对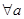 ,b∈(0,+∞),
,b∈(0,+∞),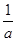 +
+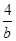 ≥|2x-1|-|x+1|恒成立,
≥|2x-1|-|x+1|恒成立,
(Ⅰ)求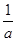 +
+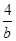 的最小值;
的最小值;
(Ⅱ)求x的取值范围。
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线 :
: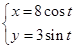 (
(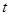 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线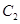 的极坐标方程为
的极坐标方程为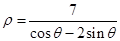 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线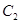 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)设 为曲线
为曲线 上的点,点
上的点,点 的极坐标为
的极坐标为 ,求
,求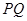 中点
中点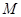 到曲线
到曲线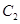 上的点的距离的最小值.
上的点的距离的最小值.
(本小题满分10分)选修4—1:几何证明选讲
如图,已知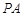 与圆
与圆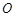 相切于点
相切于点 ,半径
,半径 ,
,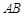 交
交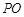 于点
于点 ,
,
(Ⅰ)求证: ;
;
(Ⅱ)若圆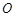 的半径为3,
的半径为3, ,求
,求 的长度.
的长度.