设函数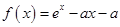 .
.
(1)若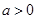 ,
, 对一切
对一切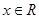 恒成立,求
恒成立,求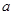 的最大值;
的最大值;
(2)设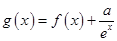 ,且
,且 、
、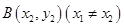 是曲线
是曲线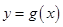 上任意两点,若对任意
上任意两点,若对任意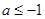 ,直线
,直线 的斜率恒大于常数
的斜率恒大于常数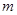 ,求
,求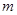 的取值范围.
的取值范围.
设数列{an}满足a1=3,an+1=an2-2nan+2,n=1,2,3,…
(1)求a2,a3,a4的值,并猜想数列{an}的通项公式(不需证明);
(2)记Sn为数列{an}的前n项和,试求使得Sn<2n成立的最小正整数n,并给出证明.
用数学归纳法证明42n+1+3n+2能被13整除,其中n∈N*.
已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明: 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
已知非零向量a,b,且a⊥b,求证: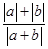 ≤
≤ .
.
已知函数f(x)=ax+ (a>1).
(a>1).
(1)证明:函数f(x)在(-1,+∞)上为增函数;
(2)用反证法证明方程f(x)=0没有负数根.