设函数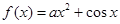 .
.
(Ⅰ)证明: 时,函数
时,函数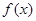 在
在 上单调递增;
上单调递增;
(Ⅱ)证明: .
.
在 ABC中,内角A,B,C的对边分别为a,b,c.
ABC中,内角A,B,C的对边分别为a,b,c.
已知 ,
, .
.
(Ⅰ)求 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求 ABC的面积.
ABC的面积.
设 是公比大于1的等比数列,
是公比大于1的等比数列,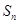 为数列
为数列 的前
的前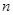 项和.已知
项和.已知 ,且
,且 构成等差数列.
构成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前
的前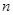 项和
项和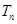 .
.
某单位有 、
、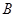 、
、 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点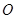 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
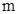 ,
,
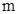 ,
,
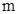 .假定
.假定 、
、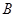 、
、 、
、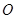 四点在同一平面内.
四点在同一平面内.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求点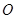 到直线
到直线 的距
的距
数列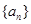 的前n项和为
的前n项和为 ,
,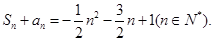
(I)证明:数列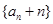 是等比数列;
是等比数列;
(Ⅱ)若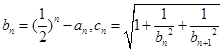 ,数列
,数列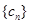 的前n项和为
的前n项和为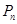 ,求不超过
,求不超过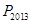 的最大整数的值.
的最大整数的值.
已知函数 .
.
(Ⅰ)当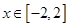 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)若对一切 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.