设函数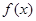 是定义在R上的奇函数,对任意实数
是定义在R上的奇函数,对任意实数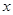 有
有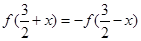 成立.
成立.
(1)证明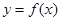 是周期函数,并指出其周期;
是周期函数,并指出其周期;
(2)若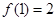 ,求
,求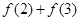 的值;
的值;
(3)若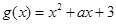 ,且
,且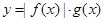 是偶函数,求实数
是偶函数,求实数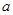 的值.
的值.
已知直线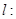
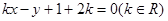 .(1)证明:直线
.(1)证明:直线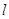 过定点;(2)若直线
过定点;(2)若直线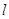 不过第四象限,求
不过第四象限,求 的取值范围;(3)若直线
的取值范围;(3)若直线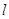 交
交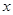 负半轴于点A,交
负半轴于点A,交 的正半轴于点B,O为坐标原点,设△ABC的面积为S,求S的最小值及此时
的正半轴于点B,O为坐标原点,设△ABC的面积为S,求S的最小值及此时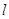 的方程.
的方程.
在 中,角
中,角 ,
, ,
,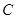 的对边分别为
的对边分别为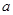 ,
,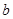 ,
, ,若
,若 .
.
(1)求证: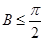 ;
;
(2)当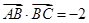 ,
, 时,求
时,求 的面积
的面积
(满分12分)已知函数 ,常数
,常数 。
。
(1)若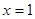 是函数
是函数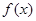 的一个极值点,求
的一个极值点,求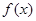 的单调区间;
的单调区间;
(2)若函数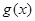
 在区间
在区间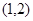 上是增函数,求
上是增函数,求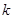 的取值范围;
的取值范围;
(3)设函数 ,求证:
,求证: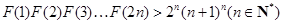
(满分12分)已知点F为抛物线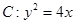 的焦点,点P时准线
的焦点,点P时准线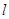 上的动点,直线PF交抛物线C于A、B两点,若点P的纵坐标为
上的动点,直线PF交抛物线C于A、B两点,若点P的纵坐标为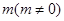 ,点D为准线
,点D为准线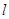 与
与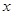 轴的交点。
轴的交点。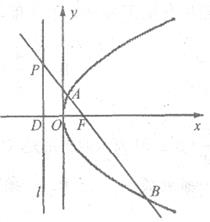
(Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S的范围;
(Ⅲ)设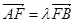 ,
,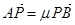 ,求证
,求证 为定值。
为定值。
(满分12分)甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为
。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)设甲、乙、丙三人中破译出密码的人数为X,求X得分布列和数学期望EX。