已知函数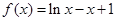 ,
,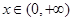 ,
,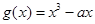 .
.
(1)求 的最大值;
的最大值;
(2)若对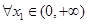 ,总存在
,总存在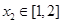 使得
使得 成立,求
成立,求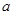 的取值范围;
的取值范围;
(3)证明不等式: .
.
(本小题满分12分)求方程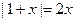 的根.
的根.
(本小题满分12分)若函数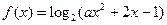 有最大值1,求实数
有最大值1,求实数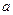 的值.
的值.
((本小题满分14分)设函数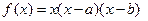 ,
, 。
。
⑴ 若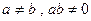 ,过两点
,过两点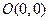 和
和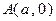 的中点作
的中点作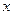 轴的垂线交曲线
轴的垂线交曲线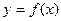 于点
于点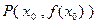 ,求证:曲线
,求证:曲线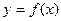 在点
在点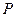 处的切线
处的切线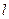 过点
过点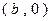 ;
;
⑵ 若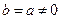 ,当
,当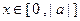 时
时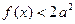 恒成立,求实数
恒成立,求实数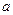 的取值范围。
的取值范围。
(本小题满分12分)
电信局为了配合客户的不同需要,设有A、B两种优惠方案,这两种方案的应付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分)(注:图中MN//CD).试问:
(Ⅰ)若通话时间为2小时,按方案A、B各付话费多少元?
(Ⅱ)方案B从500分钟后,每分钟收费多少元?
(Ⅲ)通话时间在什么范围内,方案B才会比方案A优惠?
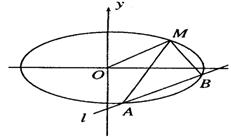
(本小题满分12分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 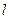 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线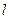 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;