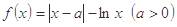 .
.
(1)若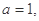 求
求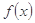 的单调区间及
的单调区间及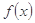 的最小值;
的最小值;
(2)试比较 与
与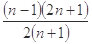 的大小.
的大小. ,并证明你的结论.
,并证明你的结论.
设f(x)=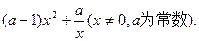
(Ⅰ)讨论f(x)的奇偶性,并说明理由;
(Ⅱ)当a=2,求f(x)的极值.
已知数列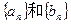 中,
中, 当
当 时,函数
时,函数 取得极值。
取得极值。
(1)求数列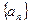 的通项公式。
的通项公式。
(2)若点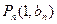 。过函数
。过函数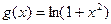 图象上的点
图象上的点 的切线始终与
的切线始终与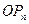 平行(O是坐标原点)。求证:当
平行(O是坐标原点)。求证:当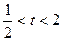 时,不等式
时,不等式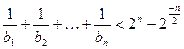 对任意
对任意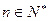
都成立。
已知函数 是偶函数,当
是偶函数,当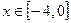 时.
时.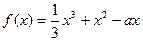 (a为实数).
(a为实数).
(1)若 在
在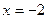 处有极值,求a的值。
处有极值,求a的值。
(2)若 在
在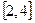 上是减函数,求a的取值范围。
上是减函数,求a的取值范围。
已知函数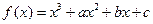 ,
, 有极值,曲线
有极值,曲线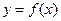
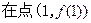 处的切线
处的切线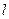 不过第四象限且斜率为3。
不过第四象限且斜率为3。
(1)求 ,
,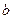 ,
,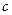 的值;
的值;
(2)求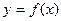 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
已知函数
(1)若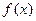 有极值,求b的取值范围;
有极值,求b的取值范围;
(2)若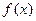 在
在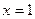 处取得极值时,当
处取得极值时,当 恒成立,求c的取值范围;
恒成立,求c的取值范围;
(3)若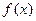 在
在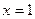 处取得极值时,证明:对[-1,2]内的任意两个值
处取得极值时,证明:对[-1,2]内的任意两个值 都有
都有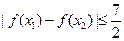 .
.