为了解今年某校高三毕业班准备报考飞行员学生体重情况，将所得的数据整理后，画出了频率分布直方图（如图）.已知图中从左到右的前3个小组的频率之比为
，其中第二小组的频数为12.
（1）求该校报考飞行员的总人数；
（2）以这所学校的样本来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选三人，设
表示体重超过60公斤的学生人数，求的分布列和数学期望.
已知函数
（1）当
时，求函数
的最小值；
（2）若对任意
恒成立，求实数
的取值范围。
已知函数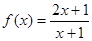
（1）判断函数在区间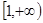
上的单调性，并用定义证明你的结论；
（2）求该函数在区间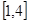
上的最大值与最小值。
已知二次函数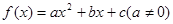
的图象过点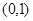
，且与x轴有唯一的交点
。
（Ⅰ）求
的表达式；
（Ⅱ）当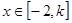
时，求函数的最小值。
(12分)已知f(x)的定义域为(0，＋∞)，且满足f(2)＝1，f(xy)＝f(x)＋f(y)，又当x2>x1>0时，f(x2)>f(x1)．
(1)求f(1)、f(4)、f(8)的值；
(2)若有f(x)＋f(x－2)≤3成立，求x的取值范围．
(12分)已知函数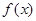
是定义在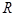
上的奇函数，当
，
（1）画出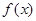图象；
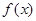（2）求出的解析式.